1.3.3 商集合
集合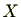 に同値関係
に同値関係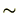 が定義されているとき、前講より集合
が定義されているとき、前講より集合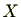 は完全代表系の元による同値類
は完全代表系の元による同値類![$ [r]$](numbertheory-img172.png) の直和で表されることがわかります。
の直和で表されることがわかります。
定義 1.3.12
集合
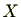
に同値関係
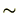
が定義されているとき、同値類全体からなる集合を
同値関係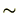 による商集合(quotient set)
による商集合(quotient set)といい、
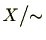
と記載します。つまり、
ここで、商集合は同値類からなる集合であるため、元の集合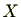 とは階層が異なることに注意しましょう。商集合
とは階層が異なることに注意しましょう。商集合
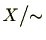 は
は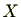 の元を同値関係
の元を同値関係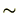 で分類した分類を要素とする集合です。このことを例を使ってみていきましょう。
で分類した分類を要素とする集合です。このことを例を使ってみていきましょう。
例 1.3.13
例1.3.10のように、年月日からなる集合
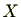
に曜日による同値関係
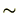
が定義されます。このとき、日曜日の集合を
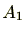
月曜日の集合を
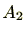
・・・、
土曜日の集合を
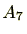
とすると、
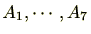
が全ての同値類ですので商集合
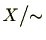
は
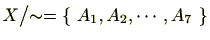
となります。
例 1.3.14 (

)
例のように,自然数
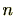
を固定すると整数
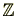
には同値関係

が定義されます。任意の整数は自然数
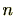
で割ると余りは
0以上
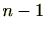
以下の整数になります。したがって,
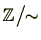
は、
![$ \{[0],[1],\cdot,[n-1]\}$](numbertheory-img197.png)
であることが分かります。
つまり、商集合とは同値類[a]を抽象化したものと考えられます。たとえば「2012年1月1日と同じ曜日の集合」を考えるよりも端的に「月曜日」を考えた方が効率的です。
Takashi
平成24年5月27日
![]() とは階層が異なることに注意しましょう。商集合
とは階層が異なることに注意しましょう。商集合
![]() は
は![]() の元を同値関係
の元を同値関係![]() で分類した分類を要素とする集合です。このことを例を使ってみていきましょう。
で分類した分類を要素とする集合です。このことを例を使ってみていきましょう。