2.2.1 多項式

本HPでは、特に断りがない場合、"多項式"とは、1変数多項式（univariate polynomial）, polynomial in one variable）を指します。「1変数多項式」とは変数（ $\mathrm{X}$ や $\mathrm{Y}$ など)が1種類である多項式のことです。

多項式の係数は、整数であったり有理数であったり実数であったり様々です。このうち、有理数を係数とする多項式を有理係数多項式（polynomial in one variable with rational coefficient）といい、有理係数多項式全体の集合を $\mathbb{Q}[X]$ と記載します。 $\mathbb{Q}$ は有理数体のこと、 $[\mathrm{X}]$ は変数を $\mathrm{X}$ とする多項式であることを意味しています（丸括弧

でなく四角括弧

であることに注意してください。丸括弧

には別の意味があります。） ${\mathrm{X}^2+2\mathrm{X}+1}$ とか、 ${3\mathrm{X}^5-1}$ などです。 $\mathrm{Y}$ を変数とする多項式であれば $\mathbb{Q}[\mathrm{Y}]$ と記載します。小文字ではなく大文字で $\mathrm{X}$ を記載するのも理由があります。これについては、後に述べます。

また、係数を整数とする多項式を、整数係数多項式といい $\mathbb{Z}[\mathrm{X}]$ と書きます。 $\mathbb{Z}$ は整数環を意味し、 $[\mathrm{X}]$ は $\mathrm{X}$ を変数等する多項式であることを意味しています。 $\mathrm{X}^{100}$ は有理係数多項式でもあり整数係数多項式でもあります。しかし、 $\sqrt{2}\mathrm{X}^2$ は有理係数多項式ではありません。

同様に、実数係数多項式を $\mathbb{R}[\mathrm{X}]$ と複素係数多項式を $\mathbb{C}[\mathrm{X}]$ と記載します。

なお、多項式には0次多項式（=定数）も含まれていることに注意してください。例えば、

や ${\textstyle \frac{1}{2}}$ は、有理数ですが0次多項式として有理係数多項式にもふくまれます。
$\mathrm{K}$ を $\mathbb{Z},\mathbb{Q},\mathbb{R},\mathbb{C}$ とすると $\mathrm{K}\subset \mathrm{K}[\mathrm{X}]$ です。

最大次数の係数が1の多項式をモニック多項式あるいはモニック（monic）であるといいます。

例 2.2.1
$\mathrm{X}^2+\mathrm{X}+1$ は、モニックです。
$2\mathrm{X}^2+\mathrm{X}+1$ はモニックではありませんが、 ${\textstyle \frac{1}{2}}$ 倍した、 ${\textstyle \mathrm{X}^2+\frac{1}{2}\mathrm{X}+1}$ はモニックです。

$\mathrm{K}$ を $\mathbb{Q},\mathbb{R},\mathbb{C}$ とすると、任意の $f(\ne0)\in \mathrm{K}[\mathrm{X}]$ に対し、

の最高次の係数を $a_n\in \mathrm{K}$ とすると、 $\frac{1}{a_n}f$ はモニックとなります。
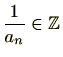これに対し、 $\mathrm{K}=\mathbb{Z}$ のときはモニックにすることができません。 $\frac{1}{a_n}\in \mathbb{Z}$ とは限らないからです。

多項式 $f(\mathrm{X})$ の次数（degree）を $\deg(f)$ で表します。ただし、

のときは便宜的に $\deg(0)=-\infty$ と定義します。定義より、 $\deg(fg)=\deg(f)+\deg(g)$ です。 $\deg(f)\leqq0$ の多項式、つまり定数項（constant term）のみからなる多項式を本HPでは定数多項式といいます。この用語は必ずしも一般的ではありません。定数多項式は $\mathrm{K}$ の元と同一視することができます。