2.3.1 X^n-1の因数分解

$\mathrm {X}^n-1$の $\mathbb{Z}[\mathrm{X}]$での因数分解を考えてみましょう。

例 2.3.1
$n=2,3,4$のときは、次のように因数分解されます。

$$\mathrm{X}^2-1 = (\mathrm{X}-1)(\mathrm{X}+1)$$ (2.1)

$$\mathrm{X}^3-1 = (\mathrm{X}-1)(\mathrm{X}^2+\mathrm{X}+1)$$ (2.2)

$$\mathrm{X}^4-1 = (\mathrm{X}^2-1)(\mathrm{X}^2+1)$$

$$= (\mathrm{X}-1)(\mathrm{X}+1)(\mathrm{X}^2+1)$$ (2.3)

$\mathrm{X}^2+\mathrm{X}+1=0$や $\mathrm{X}^2+1=0$は有理数解を持たないので、式2.2や式2.3は、 これ以上分解できないことがわかります。

$\mathrm{X}^n-1=0$は $\mathrm{X}=1$を解にもつため、 $\mathrm{X}-1$で割り切れます。

命題 2.3.2

$$\mathrm{X}^n-1=(\mathrm{X}-1)(\mathrm{X}^{n-1}+\mathrm{X}^{n-2}+\cdots+\mathrm{X}+1)$$

証明
右辺を展開すると $(\mathrm{X}^n+\mathrm{X}^{n-1}+\cdots+\mathrm{X}^2+\mathrm{X})-(\mathrm{X}^{n-1}+\mathrm{X}^{n-2}+\cdots+\mathrm{X}+1)=\mathrm{X}^n-1$となり左辺と一致する。

$n=5$以上の場合の $\mathrm {X}^n-1$の因数分解を考えます。

• $n=5$の場合。 上記命題より、

  $$\mathrm{X}^5-1=(\mathrm{X}-1)(\mathrm{X}^4+\mathrm{X}^3+\mathrm{X}^2+\mathrm{X}+1)$$ (2.4)

  
  
  です。それでは、 $\mathrm{X}^4+\mathrm{X}^3+\mathrm{X}^2+\mathrm{X}+1$は既約でしょうか。仮に、 $\mathrm{X}^4+\mathrm{X}^3+\mathrm{X}^2+\mathrm{X}+1$が1次式を因子に持つと仮定すると、定理2.2.8より整数解がありますが、他方、補題2.2.28より整数解の可能性があるのは$\pm 1$だけです。よって、 $\mathrm{X}^4+\mathrm{X}^3+\mathrm{X}^2+\mathrm{X}+1=0$に整数解はありませんので1次式で因数分解することはできません。
  すると、因数分解ができる可能性がルのは2次式×2次式に限られることになりますが、そのような分解は可能でしょうか。地道な方法になりますが、仮に、2次式×2次式に分解できると仮定して（例えば、 $(\mathrm{X}^2+a\mathrm{X}+b)(\mathrm{X}^2+c\mathrm{X}+d)$（ここで、$a,b,c,d$は整数）と分解できると仮定しこれを展開したものと、 $\mathrm{X}^4+\mathrm{X}^3+\mathrm{X}^2+\mathrm{X}+1$の各係数を比べ、そのような$a,b,c,d$は（整数では）存在しないことを示すことによってできます。）

• $n=6$のとき
  

  $$\mathrm{X}^6-1 = (\mathrm{X}^3-1)(\mathrm{X}^3+1)$$

  $$= (\mathrm{X}-1)(\mathrm{X}^2+\mathrm{X}+1)(\mathrm{X}+1)(\mathrm{X}^2-\mathrm{X}+1)$$ (2.5)

  
  となります。 $(\mathrm{X}^2+\mathrm{X}+1)と(\mathrm{X}^2-\mathrm{X}+1)$は、整数解をもたないことから既約であることがわかり、この分解が既約分解であることがわかります。

• $n=7$のとき命題2.3.2より

  $$\mathrm{X}^7-1=(\mathrm{X}-1)(\mathrm{X}^6+\mathrm{X}^5+\mathrm{X}^4+\mathrm{X}^3+\mathrm{X}^2+\mathrm{X}+1)$$ (2.6)

  
  

  $(\mathrm{X}^6+\mathrm{X}^5+\mathrm{X}^4+\mathrm{X}^3+\mathrm{X}^2+\mathrm{X}+1)$は既約多項式でしょうか。これまでと同様に、整数解をもたないことが分かりますので、1次式を因数に持たないことがわかります。すると、考えられる分解は、2次式×4次式、2次式×2次式×2次式、3次×3次式ですので、$n=5$の場合と同様に整数係数多項式に分解できると仮定し、分解できるかどうか確かめることができますが、この方法は、非常に多数の連立方程式を解くことになり、見通しはよくありません。見通しよく解決することはできないでしょうか。

  ここでは、$n=7$の場合は置いておいて、$n=8$以上の場合にどう分解されるのか確かめてみましょう。それにより、$n=7$の場合の解決の方法が見通せるかもしれません。このように、数学の問題にぶつかった時は、より問題を一般化することにより、具体的な問題の解決のヒントが見つかることがよくあります。

• $n=8$のとき
  

  $$\mathrm{X}^8-1 = (\mathrm{X}^4-1)(\mathrm{X}^4+1)$$

  $$= (\mathrm{X}^2-1)(\mathrm{X}^2+1)(\mathrm{X}^4+1)$$

  $$= (\mathrm{X}-1)(\mathrm{X}+1)(\mathrm{X}^2+1)(\mathrm{X}^4+1)$$ (2.7)

  
  

  と分解されます。 $(\mathrm{X}^4+1)$は、これまでと同様に既約多項式であることが示せます。

• $n=9$のとき
  

  $$\mathrm{X}^9-1 = (\mathrm{X}^3-1)(\mathrm{X}^6+\mathrm{X}^3+1)$$

  $$= (\mathrm{X}-1)(\mathrm{X}^2+\mathrm{X}+1)(\mathrm{X}^6+\mathrm{X}^3+1)$$ (2.8)

  
  

  と分解されます。ここで、 $(\mathrm{X}^6+\mathrm{X}^3+1)$が既約多項式か問題になりますが、その点はおいておきましょう。

• $n=10$のとき
  

  $$\mathrm{X}^{10}-1 = (\mathrm{X}^5-1)(\mathrm{X}^5+1)$$

  $$= (\mathrm{X}-1)(\mathrm{X}^4+\mathrm{X}^3+\mathrm{X}^2+\mathrm{X}+1)(\mathrm{X}^5+1)$$

  $$= (\mathrm{X}-1)(\mathrm{X}^4+\mathrm{X}^3+\mathrm{X}^2+\mathrm{X}+1)(\mathrm{X}+1)(\mathrm{X}^4-\mathrm{X}^3+\mathrm{X}^2-\mathrm{X}+1)$$

  
  と分解されます

• $n=11$のとき
  

  $$\mathrm{X}^{11}-1=(\mathrm{X}-1)(\mathrm{X}^{10}+\mathrm{X}^9+\mathrm{X}^8+\cdots+\mathrm{X}^3+\mathrm{X}^2+\mathrm{X}+1)$$ (2.9)

  
  $(\mathrm{X}^{10}+\mathrm{X}^9+\mathrm{X}^8+\cdots+\mathrm{X}^3+\mathrm{X}^2+\mathrm{X}+1)$が既約であるか否かはここではおいておきましょう。

• $n=12$のとき
  

  $$\mathrm{X}^{12}-1 = ((\mathrm{X}^4)^3-1)$$

  $$= (\mathrm{X}^4-1)(\mathrm{X}^8+\mathrm{X}^4+1)$$

  
  ここで、 $(\mathrm{X}^4-1)$は式2.3より $(\mathrm{X}-1)(\mathrm{X}+1)(\mathrm{X}^2+1)$です。
  $(\mathrm{X}^8+\mathrm{X}^4+1)$の因数分解はテクニックが必要です。
  
  

  $$(\mathrm{X}^8+\mathrm{X}^4+1) = (\mathrm{X}^8+2\mathrm{X}^4+1)-\mathrm{X}^4$$

  $$= (\mathrm{X}^4+1)^2-\mathrm{X}^4$$

  $$= (\mathrm{X}^4+1-\mathrm{X}^2)(\mathrm{X}^4+1+\mathrm{X}^2)$$

  $$= (\mathrm{X}^4-\mathrm{X}^2+1)(\mathrm{X}^4+\mathrm{X}^2+1)$$

  
  以上をまとめると、
  $$\mathrm{X}^{12}-1=(\mathrm{X}-1)(\mathrm{X}+1)(\mathrm{X}^2+1)(\mathrm{X}^2+\mathrm{X}+1)(\mathrm{X}^2-\mathrm{X}+1)(\mathrm{X}^4-\mathrm{X}^2+1)$$

ここまで、$n=2〜12$まで、 $\mathrm {X}^n-1$の因数分解をみてきました、何か法則はあるでしょうか。 見通しをよくするためにここまでの結果を表にまとめてみます。

表 2.3: $\mathrm {X}^n-1$の因数分解

この表からなにか分かることがあるでしょうか。因子の個数に着目すると$n=2,3,5,7$の場合のように2つにしか分解されないものもあれば、$n=6,8,10$のように多数の因子に分解されるものがあることが分かります。例えば、$n=8$の場合は、 $\mathrm{X}^8-1=(\mathrm{X}^4)^2-1$と分解できますので、 $(\mathrm{X}^4+1)(\mathrm{X}^4-1)$と分解でき、 $(\mathrm{X}^4-1)$を因数分解することによりさらなる分解ができますね。つまり、これは、 $n=8=4\times 2$と分解できることに由来しています。これに対し、$n=7$の場合は、$7$をこれ以上分解できないことから、 $(\mathrm{X}-1)(\mathrm{X}^6+\mathrm{X}^5+\mathrm{X}^4+\mathrm{X}^3+\mathrm{X}^2+\mathrm{X}+1)$もこれ以上分解できないことが想像されます。 つまり、 $\mathrm {X}^n-1$の因数分解は、$n$の素因数分解に関係していそうだということがわかります。したがって、 $\mathrm {X}^n-1$の因数分解を調べるには、$n$の素因数分解を調べることが有用そうです。

また、同じ式がいくつか出てきていることが分かりますね。例えば、 $\mathrm{X}^4-1$の因数分解には、 $\mathrm{X}^2-1$の因数が含まれていますし、 $\mathrm{X}^9-1$の因数分解には、 $\mathrm{X}^3-1$の因数が含まれています。同様に $\mathrm{X}^6-1$の因数分解には、 $\mathrm{X}^2-1$の因数と $\mathrm{X}^3-1$の因数が含まれています。このように、 $\mathrm {X}^n-1$の因数分解には、$n$の約数を$d$としたときの $\mathrm{X}-^d-1$の因数分解が含まれていると予想できますね。

$$\mathrm{X}^n-1の因数分解 \overset{対応}{\longleftrightarrow} nの素因数分解$$

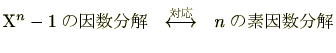
次項ではこれを見ていきましょう。