Next: 2.3.3 原始n乗根 Up: 2.3 円分多項式 Previous: 2.3.1 X^n-1の因数分解
命題2.3.2より
![]() ですのでの解の1つは1となります。
ですのでの解の1つは1となります。
![]() の解は、補題2.2.28より整数解の可能性があるのは
の解は、補題2.2.28より整数解の可能性があるのは![]() に限りますが、
に限りますが、![]() は整数解ではありませんので、整数解はありません。(したがって、定理
は整数解ではありませんので、整数解はありません。(したがって、定理![[*]](crossref.png) より有理数解がないことが分かります。)
より有理数解がないことが分かります。)
![]() の解を
の解を![]() とすると
とすると
![]() ですので、
ですので、![]() 乗して1になる数、つまり、1の
乗して1になる数、つまり、1の![]() 乗根です。
乗根です。
![]() は
は![]() 次式ですので複素数上解は
次式ですので複素数上解は![]() 個あります。
個あります。
![]() が小さいときに、1の
が小さいときに、1の![]() 乗根を具体的に求めてみましょう。
乗根を具体的に求めてみましょう。
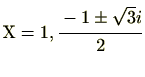 です。
です。
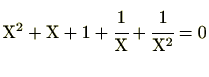 |
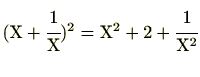 ですので、
ですので、
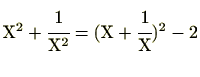 となります。これを、上の式に代入すると、
となります。これを、上の式に代入すると、
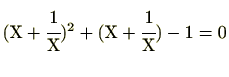 |
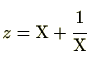 とすると、
とすると、
| (2.10) |
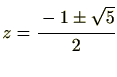 となります。
となります。
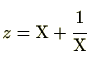 ですので、これを
ですので、これを
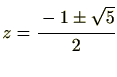 を代入すると
を代入すると
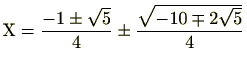
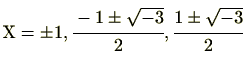 です。
です。
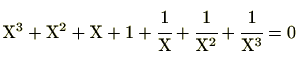 |
(2.11) |
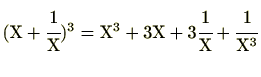 つまり、
つまり、
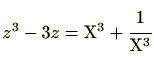 であることに留意すると、円周等分方程式は
であることに留意すると、円周等分方程式は
![\begin{multline*}
\frac{1}{12}\left(-2+\sqrt[3]{28+84\sqrt{-3}}+\sqrt[3]{28+84\s...
...+4\sqrt[3]{28+84\sqrt{-3}}+\sqrt[3]{(28+84\sqrt{-3})^2}}\right)
\end{multline*}](numbertheory-img747.png)
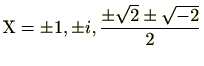
Takashi