2.2.8 整数係数多項式
ここまでは主に体(
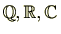 )係数多項式を考えてきましたが、最後に整数係数多項式を考えます。整数係数多項式を考える上で基本となるのはガウスの補題です。ガウスの補題を用いることにより、
)係数多項式を考えてきましたが、最後に整数係数多項式を考えます。整数係数多項式を考える上で基本となるのはガウスの補題です。ガウスの補題を用いることにより、
![$ \mathbb{Z}[\mathrm{X}]$](numbertheory-img462.png) 既約であれば、
既約であれば、
![$ \mathbb{Q}[\mathrm{X}]$](numbertheory-img502.png) 上も既約であることが示されます。
上も既約であることが示されます。
整数係数多項式環
![$ \mathbb{Z}[\mathrm{X}]$](numbertheory-img462.png) においても、定義2.2.5により正則元や既約多項式が定義できます。しかし、体係数多項式の場合と異なり、正則元は定数多項式とは一致しません。
においても、定義2.2.5により正則元や既約多項式が定義できます。しかし、体係数多項式の場合と異なり、正則元は定数多項式とは一致しません。
命題 2.2.21
![$ \mathbb{Z}[\mathrm{X}]$](numbertheory-img462.png)
の正則元は
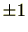
のみである。(
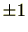
は定数多項式として
![$ \mathbb{Z}[\mathrm{X}]$](numbertheory-img462.png)
の元であることに注意)
定義 2.2.22
整数係数多項式
![$ f(\mathrm{X})=a_n\mathrm{X}^n+a_{n-1}\mathrm{X}^{n-1}+\cdots+a_1\mathrm{X}+a_0\in \mathbb{Z}[\mathrm{X}]$](numbertheory-img586.png)
の係数の最大公約数
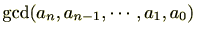
が1であるとき、
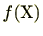
は
原始的(primitive)であるという。
例 2.2.23
(1)
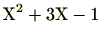
はprimitiveである。
(2)
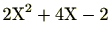
はprimitiveでない。
命題 2.2.24
![$ f\in\mathbb{Z}[\mathrm{X}]$](numbertheory-img590.png)
の元が既約である場合下記(1)(2)のいずれかである。
逆に下記(1)または(2)が成り立つ場合、
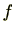
は
![$ \mathbb{Z}[\mathrm{X}]$](numbertheory-img462.png)
の元として既約である。
(1)
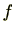
は
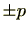
(
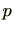
:素数)
(2)
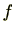
はprimitiveで
![$ f=gh(g,h\in\mathbb{Z}[\mathrm{X}] )$](numbertheory-img592.png)
と分解できるのは
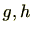
のいずれかが
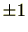
のときに限る。
補題 2.2.25
![$ f\in\mathbb{Q}[\mathrm{X}]$](numbertheory-img594.png)
で
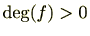
とすると、有理数
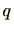
が存在して
![$ qf\in \mathbb{Z}[\mathrm{X}]$](numbertheory-img596.png)
をprincipleとすることができる。
証明
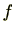
の係数を既約分数で表したときの分母の最小公倍数を
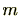
とし、分子の最大公約数を
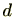
とし、
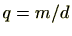
とすると
![$ qf\in \mathbb{Z}[\mathrm{X}]$](numbertheory-img596.png)
で
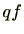
はprincipleとなる。
補題 2.2.26 (ガウスの補題)
![$ f,g\in\mathbb{Z}[\mathrm{X}]$](numbertheory-img599.png)
がprincipleのとき、
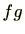
もprincipleである。
証明
(
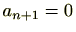
等と定義することにより、全ての自然数iに対し、
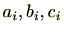
を定義する。)
仮に
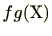
がprincipleでないとき、
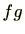
の係数の最大公約数の素因子を
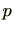
とすると、任意
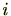
に対し
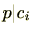
である。他方、
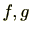
はprincipleであるため、
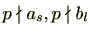
となる
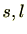
が存在するため、
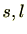
をそのようなもので最大なものとする。すると、
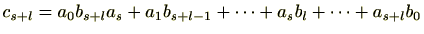
であり、
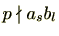
であるがそれ以外の項は仮定より
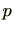
で割り切れる。
したがって、
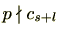
。これは仮定に矛盾する。
定理 2.2.27
![$ f\in\mathbb{Z}[\mathrm{X}]$](numbertheory-img590.png)
が
![$ \mathbb{Z}[\mathrm{X}]$](numbertheory-img462.png)
の元として既約で、
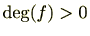
であるとき、
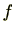
は
![$ \mathbb{Q}[\mathrm{X}]$](numbertheory-img502.png)
の元としても既約である。
逆に、
![$ f\in\mathbb{Z}[\mathrm{X}]$](numbertheory-img590.png)
が
![$ \mathbb{Q}[\mathrm{X}]$](numbertheory-img502.png)
の元として既約でprincipleである場合、
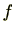
は
![$ \mathbb{Z}[\mathrm{X}]$](numbertheory-img462.png)
の元としても既約である。
上の定理より、
![$ \mathbb{Z}[\mathrm{X}]$](numbertheory-img462.png) の既約と
の既約と
![$ \mathbb{Q}[\mathrm{X}]$](numbertheory-img502.png) の既約は本質的に同じであり、同一視しても良いことが分かりました。
の既約は本質的に同じであり、同一視しても良いことが分かりました。
これにより、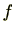 が一次式で割り切れるかは
が一次式で割り切れるかは
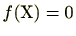 が有理数解を持つか否かできまります。
次の補題は
が有理数解を持つか否かできまります。
次の補題は
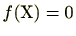 の有理数解を絞るうえで重要な補題です。
の有理数解を絞るうえで重要な補題です。
補題 2.2.28
![$ f\in\mathbb{Z}[\mathrm{X}]$](numbertheory-img590.png)
が一次式
$](numbertheory-img628.png)
で割り切れる場合、

は
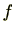
の最高次係数の約数であり、
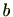
は
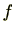
の定数項の約数である。
例えば、最高次係数が1(つまりモニック)の多項式の場合は、定数項の約数のみが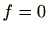 の解の候補になります。
の解の候補になります。
定義 2.2.29
モニックな整数係数多項式
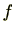
に対し
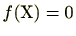
の解を
代数的整数といい、代数的整数全体の集合を
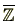
と表す。
Remark 2.2.30
後に見るように代数的整数からなる集合
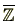
は環をなします。
代数的整数に対し、通常の整数を有理整数ということがあります。
有理整数 は、
は、
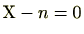 の解ですので代数的整数です。逆に有理数でかつ代数的整数は有理整数に限ります。
の解ですので代数的整数です。逆に有理数でかつ代数的整数は有理整数に限ります。
定理 2.2.31
有理数で代数的整数は有理整数に限る。つまり、
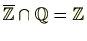
例 2.2.32
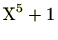
は
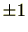
を解として持たないため、一次式で割り切れない。
Takashi
平成24年5月27日
![]() においても、定義2.2.5により正則元や既約多項式が定義できます。しかし、体係数多項式の場合と異なり、正則元は定数多項式とは一致しません。
においても、定義2.2.5により正則元や既約多項式が定義できます。しかし、体係数多項式の場合と異なり、正則元は定数多項式とは一致しません。
![]() が
が
![]() の元として既約でprincipleであると仮定すると、
の元として既約でprincipleであると仮定すると、![]() である。仮に、
である。仮に、
![]() と分解できたと仮定すると、
と分解できたと仮定すると、![]() が
が
![]() の元として既約であることより
の元として既約であることより![]() のいずれかは定数多項式であるが、他方、
のいずれかは定数多項式であるが、他方、![]() がprincipleであることにより、いずれかは
がprincipleであることにより、いずれかは![]() である。よって
である。よって![]() は
は
![]() の元としても既約である。
の元としても既約である。
![]() の既約と
の既約と
![]() の既約は本質的に同じであり、同一視しても良いことが分かりました。
の既約は本質的に同じであり、同一視しても良いことが分かりました。
![]() が一次式で割り切れるかは
が一次式で割り切れるかは
![]() が有理数解を持つか否かできまります。
次の補題は
が有理数解を持つか否かできまります。
次の補題は
![]() の有理数解を絞るうえで重要な補題です。
の有理数解を絞るうえで重要な補題です。
![]() の解の候補になります。
の解の候補になります。
![]() は、
は、
![]() の解ですので代数的整数です。逆に有理数でかつ代数的整数は有理整数に限ります。
の解ですので代数的整数です。逆に有理数でかつ代数的整数は有理整数に限ります。