Next: 3. 代数学の基礎 Up: 2.5 平方剰余の相互法則 Previous: 2.5.4 第2補充法則の証明
有限体上のガウス和を考えましょう。具体的には、有限体
![]() (
(![]() は奇素数)のガウス和
は奇素数)のガウス和
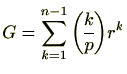 を考えます。
また、
を考えます。
また、
![]() とおきます。すると、
とおきます。すると、![]() が、
が、
![]() 上で成立しています。
上で成立しています。
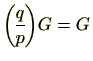 |
|||
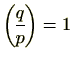 |
他方、
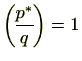 |
|||
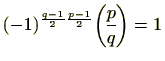 |
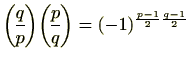 となり、証明ができました。
となり、証明ができました。
![]() 上の円分拡大体
上の円分拡大体
![]() は、ガロア拡大であり、ガロア群
は、ガロア拡大であり、ガロア群
![]() は、
は、
![]() と同型で、その同型対応は、
と同型で、その同型対応は、
そして、
![]() は巡回群ですので
は巡回群ですので![]() のとき位数
のとき位数![]() の部分群がただ一つ存在しますのでそのような部分郡を
の部分群がただ一つ存在しますのでそのような部分郡を![]() とすると、部分体
とすると、部分体
![]() は、ガロア群の指数2の部分群
は、ガロア群の指数2の部分群
![]() に対応します。
に対応します。
![$\displaystyle \xymatrix{
\mathbb{Q}(\zeta_p) \ar@{-}[d] & \{ 1\} \ar@{-}[d] & ...
...a_p)/\mathbb{Q}) &(\mathbb{Z}/p\mathbb{Z})^{\times}\ar@{}[l]\vert{\cong} \
}
$](numbertheory-img1251.png)
そして、ここからが、類体論的な事象ですが、円分体論より、上記の自然の同型対応は、アルティン写像![]() となります。アルティン写像の性質より、
となります。アルティン写像の性質より、![]() を
を![]() と異なる素数とするとき
と異なる素数とするとき
![]() 拡大体
拡大体
![]() の定義多項式が法
の定義多項式が法![]() で完全分解するが成り立ちます。(まさにこれが類体論です!)
で完全分解するが成り立ちます。(まさにこれが類体論です!)
Takashi