Next: 2.5.5 平方剰余の相互法則の証明 Up: 2.5 平方剰余の相互法則 Previous: 2.5.3 ガウス和
ここで、1の原始8乗根の1つとして
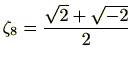 を考えましょう。(ガウス平面で考えると、)
を考えましょう。(ガウス平面で考えると、)
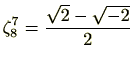 であることが分かります。したがって、
であることが分かります。したがって、
![]() です。つまり、
です。つまり、
![]() は、
は、![]() の解です。
の解です。
これと同様のことを有限体上
![]() 上で考えてみましょう。十分大きな
上で考えてみましょう。十分大きな![]() をとれば、
をとれば、![]() とできますので、
とできますので、
![]() 上の元で位数8の元を
上の元で位数8の元を![]() としましょう。(この様な元があることは、章参照。)
としましょう。(この様な元があることは、章参照。)
すると、
![]() です。(なぜなら、
です。(なぜなら、![]() は、位数8の元ですので
は、位数8の元ですので![]() です。)なお、ここで等号は、すべて、
です。)なお、ここで等号は、すべて、
![]() で考えています。
で考えています。
つまり、
![]() は、方程式
は、方程式![]() の解であることが分かります。したがって、
の解であることが分かります。したがって、
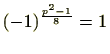 |
Takashi