Next: 2.3.4 オイラー関数 Up: 2.3 円分多項式 Previous: 2.3.2 1のn乗根
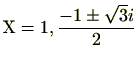 で、このうち
で、このうち
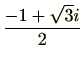 の2つが原始3乗根です。
の2つが原始3乗根です。
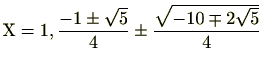 (最初の
(最初の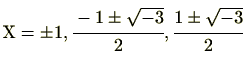 であり、このうち、
であり、このうち、
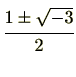 の2つが原始6乗根である。
の2つが原始6乗根である。
原始![]() 乗根はいくつあるでしょうか?
乗根はいくつあるでしょうか?
1の![]() 乗根は
乗根は![]() 個あります(Remark2.3.3参照)。ここで、1の
個あります(Remark2.3.3参照)。ここで、1の![]() 乗根
乗根![]() が何乗して初めて1になるか考えてみましょう。このように、何乗して初めて1になる、何乗のことを、指数といいます。
が何乗して初めて1になるか考えてみましょう。このように、何乗して初めて1になる、何乗のことを、指数といいます。
原始![]() 乗根の定義より、
乗根の定義より、
1の原始![]() 乗根の1つを
乗根の1つを![]() とおきます。1の原始
とおきます。1の原始![]() 乗根は必ず存在します。
乗根は必ず存在します。
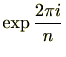 は1の
は1の
1の![]() 乗根は
乗根は![]() の形で表されますので、このうちどのようなものが原始
の形で表されますので、このうちどのようなものが原始![]() 乗根になるのか考えてみましょう。
乗根になるのか考えてみましょう。
この定理により1の原始![]() 乗根の個数は、1から
乗根の個数は、1から![]() までの自然数のうち
までの自然数のうち![]() と互いに素なもの個数と等しいことが分かります。1から
と互いに素なもの個数と等しいことが分かります。1から![]() までの自然数のうち
までの自然数のうち![]() と互いに素なもの個数を
と互いに素なもの個数を![]() で表しオイラー関数といいます。オイラー関数については、次講で詳しくみていきましょう。
で表しオイラー関数といいます。オイラー関数については、次講で詳しくみていきましょう。
Takashi