2.4.1 合同式
自然数 を固定します。ここでは、整数を
を固定します。ここでは、整数を で割った余りにより分類することを考えます。
で割った余りにより分類することを考えます。
定義 2.4.1
2つの整数
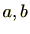
の差が

の倍数のとき、

と
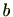
は
 を法として互いに合同(congruent modulo
を法として互いに合同(congruent modulo  )
)といい、
と記します。

は(モッドエヌ)とよみます。
また、
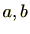
の差が

の倍数ではないとき、
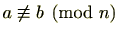
と書きます。
例 2.4.2
(1)
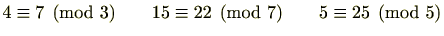
(2)
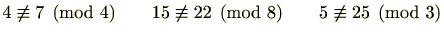
上の式には がついているため
がついているため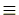 の代わりに
の代わりに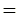 を使っても混同しませんので、
を使っても混同しませんので、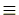 の代わりに
の代わりに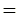 を使うことがあります。つまり、
を使うことがあります。つまり、
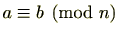 と
と
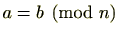 は同じ意味です。また、前後の文脈から明らかな場合は
は同じ意味です。また、前後の文脈から明らかな場合は も省略することもあります。
も省略することもあります。
 が使われている式のことを
が使われている式のことを を法とする合同式(congruence equation)といいます。
を法とする合同式(congruence equation)といいます。
次の命題は、 の性質を
の性質を で割った余りが等しいことに言い換えています。
で割った余りが等しいことに言い換えています。
命題 2.4.3
自然数

を固定し
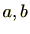
を整数とすると、
証明

を

で割ったときの余りを
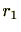
、
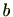
を

で割ったときの余りを
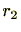
とすると、
となるような整数
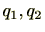
が存在します。したがって、
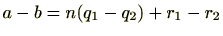
です。ここで、
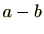
が

の倍数であるとすると、
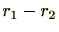
が

の倍数である必要がありますが、
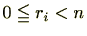
ですので
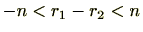
でありこの範囲で

の倍数は
0しかありませんので、
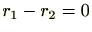
つまり余りが等しいことが分かります。
逆に、余りが等しい(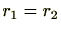 )と仮定すると、上の式より
)と仮定すると、上の式より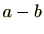 が
が の倍数であることが分かります。
の倍数であることが分かります。
次の命題は、合同式は、
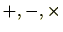 に関する限り
に関する限り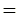 と同様に取り扱うことができることを意味しています。
と同様に取り扱うことができることを意味しています。
証明
(1)仮定より
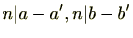
よって、
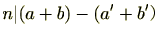
であり、これは、
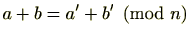
を意味する。
(2)仮定より
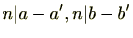
よって、
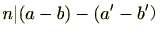
であり、これは、
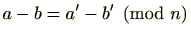
を意味する。
(3)仮定より
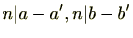
よって、
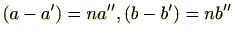
となる整数
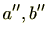
が存在する。よって、
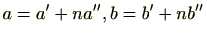
。両辺をかけると
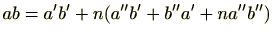
よって、
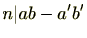
。
この定理を使うことにより次のような基本的な整数の性質を簡単に示すことができます。
例 2.4.5 (法2の場合)

を偶数とすると
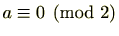
、
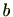
を奇数とすると
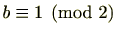
です。
上記の命題より、
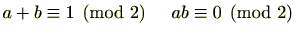
です。
これは、偶数+奇数=奇数、偶数×奇数=偶数を意味しています。同様に、偶数+偶数=偶数、奇数+奇数=偶数、奇数×奇数=奇数などを示すことができます。
例 2.4.6 (法3の場合)
整数を3で割った余りは、0、1、2のいずれかになります。
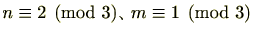
とすると、
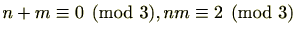
となります。
つまり、3で割ったときの余りが2の整数と余りが1の整数を足すと余りは0となる(つまり3の倍数となる)ことが分かります。また、掛けると余りは2となることが分かります。
次の例では1次合同式
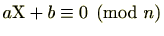 が解ける場合があることが分かります。どのような場合に解けるかについては、を参照してください。
が解ける場合があることが分かります。どのような場合に解けるかについては、を参照してください。
例 2.4.7 (一次合同式)
1次合同式
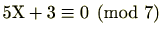
を解いてみましょう。
両辺に
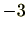
を足すことにより、
よって、
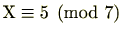
が解です。
例 2.4.8
1次合同式
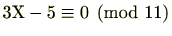
を解いてみましょう。
両辺に
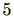
を足すことにより、
よって、
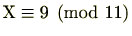
が解です。
例2.4.7では、
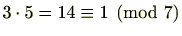 を使うことにより合同式を解きました。例2.4.8では、
を使うことにより合同式を解きました。例2.4.8では、
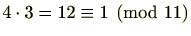 を使うことにより合同式を解きました。常にこのようにうまくいくとは限りません。
を使うことにより合同式を解きました。常にこのようにうまくいくとは限りません。
例 2.4.9
1次合同式
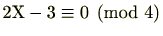
を解いてみましょう。
両辺に3を足すことにより
ここで、
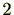
に何かをかけて
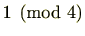
にしたいところですが、そのような数字は見つかりません。なぜでしょうか。
左辺は2の倍数ですから必ず偶数です。偶数を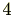 で割ると余りは0か2です。したがって、余りが3になることはありません。
で割ると余りは0か2です。したがって、余りが3になることはありません。
よって、1次合同式
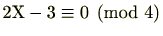 の解はありません。
の解はありません。
上の例からも1次合同式がどのような場合に解けるのか、予想してみましょう。こたえは2.4.4で扱います。また、2次合同式は解けるのか知りたいですね。2次合同式が解けるか否かをあつかったのはGaussであり、平方剰余の相互法則という極めて美しい結果があります。平方剰余の相互法則は本章の目標の1つです。
Takashi
平成24年5月27日
![]() がついているため
がついているため![]() の代わりに
の代わりに![]() を使っても混同しませんので、
を使っても混同しませんので、![]() の代わりに
の代わりに![]() を使うことがあります。つまり、
を使うことがあります。つまり、
![]() と
と
![]() は同じ意味です。また、前後の文脈から明らかな場合は
は同じ意味です。また、前後の文脈から明らかな場合は![]() も省略することもあります。
も省略することもあります。
![]() が使われている式のことを
が使われている式のことを![]() を法とする合同式(congruence equation)といいます。
を法とする合同式(congruence equation)といいます。
![]() の性質を
の性質を![]() で割った余りが等しいことに言い換えています。
で割った余りが等しいことに言い換えています。
![]() )と仮定すると、上の式より
)と仮定すると、上の式より![]() が
が![]() の倍数であることが分かります。
の倍数であることが分かります。
![]() に関する限り
に関する限り![]() と同様に取り扱うことができることを意味しています。
と同様に取り扱うことができることを意味しています。
![]() が解ける場合があることが分かります。どのような場合に解けるかについては、を参照してください。
が解ける場合があることが分かります。どのような場合に解けるかについては、を参照してください。
![]() を使うことにより合同式を解きました。例2.4.8では、
を使うことにより合同式を解きました。例2.4.8では、
![]() を使うことにより合同式を解きました。常にこのようにうまくいくとは限りません。
を使うことにより合同式を解きました。常にこのようにうまくいくとは限りません。
![]() で割ると余りは0か2です。したがって、余りが3になることはありません。
で割ると余りは0か2です。したがって、余りが3になることはありません。
![]() の解はありません。
の解はありません。