演算が定義されている集合 を考えましょう。環や体には演算が2つ(
を考えましょう。環や体には演算が2つ(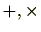 )定義されていますが、群になるために必要な演算は1つだけでたります。2つの演算が定義されていてる場合でもいずれか1つの演算を考えることにより、群になることもあります。実際、実数
)定義されていますが、群になるために必要な演算は1つだけでたります。2つの演算が定義されていてる場合でもいずれか1つの演算を考えることにより、群になることもあります。実際、実数
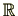 には加法、乗法という2つの演算(
には加法、乗法という2つの演算(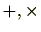 )が定義されていますが、加法に関して群となります。これに対し、
)が定義されていますが、加法に関して群となります。これに対し、
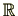 は乗法に関しては群となりません。
は乗法に関しては群となりません。
定義 3.1.2 (群)
演算
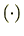
が定義されている集合

が次の条件をみたすとき

は
群(Group)であるという。
(1)(結合法則)

の任意の元
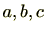
に対し
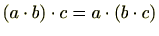
(2)(単位元の存在)

の特殊な元
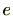 単位元
単位元が存在し、

の任意の元

に対し
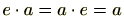
が成り立つ。
(3)(逆元の存在)

の任意の元

に対し

の元
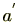
が存在し、
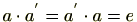
が成り立つ。
結合法則
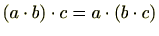 は、
は、
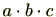 の演算の順序を気にする必要が無いことを意味しています。したがって、3つ以上の演算を考える場合でも
の演算の順序を気にする必要が無いことを意味しています。したがって、3つ以上の演算を考える場合でも
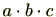 のように括弧をつける必要はありません。結合法則は、演算を考える際には最も基本的な性質です。
のように括弧をつける必要はありません。結合法則は、演算を考える際には最も基本的な性質です。
群 を考える際の演算は1つに固定されますので特に演算記号を強調する必要がないときは演算記号
を考える際の演算は1つに固定されますので特に演算記号を強調する必要がないときは演算記号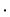 を省略し、
を省略し、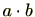 のことを
のことを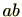 と記載します。また、
と記載します。また、 と
と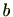 の演算をとり
の演算をとり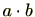 とすることを
とすることを に
に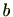 を右からかけるまたは
を右からかけるまたは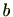 に
に を左からかけるといいます。「かける」という用語を使っています、自然数などに定義されている「乗法」とは限りません。
を左からかけるといいます。「かける」という用語を使っています、自然数などに定義されている「乗法」とは限りません。
また、交換法則
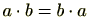 は成り立つとは限りませんので、例えば、
は成り立つとは限りませんので、例えば、 と
と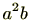 は異なるかもしれません。したがって、
は異なるかもしれません。したがって、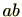 に
に をかけるというのときに、左から
をかけるというのときに、左から をかけると右から
をかけると右から をかけるとでは結果が異なる場合があります。したがって、単に
をかけるとでは結果が異なる場合があります。したがって、単に をかけるというのは意味がなく、右からかけるのか左からかけるのか明確にする必要があります。
をかけるというのは意味がなく、右からかけるのか左からかけるのか明確にする必要があります。
集合 が群であるとき、演算が定義されていますので、
が群であるとき、演算が定義されていますので、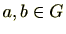 に対し
に対し
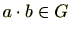 です。これを0番目の条件と考えると、集合
です。これを0番目の条件と考えると、集合 が群であるときは(0)から(3)までの4つの条件を満たす必要があります。以下で
が群であるときは(0)から(3)までの4つの条件を満たす必要があります。以下で が群であることを確かめるとき、(条件0)から(条件4)を満たしていることを確かめていきます。ある集合が群となるには、この4つの条件を満たす必要があることはよく頭に入れておきましょう。
が群であることを確かめるとき、(条件0)から(条件4)を満たしていることを確かめていきます。ある集合が群となるには、この4つの条件を満たす必要があることはよく頭に入れておきましょう。
命題 3.1.3

を群とすると、次が成り立つ。
(1)単位元はただ一つ存在する。
(2)

の任意の元

に対し

の逆元
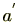
はただ一つ存在する。

のただ一つの逆元を
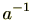
と記載する。
(3)単位元
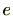
の逆元は単位元自身である。つまり、
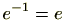
(4)

の逆元
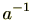
の逆元
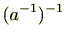
は

である。つまり
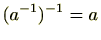
(5)
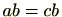
であるとき
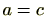
。また、
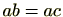
であるとき
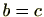
が成り立つ。
証明
(1)
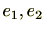
が単位元とすると、単位元の定義から、
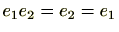
よって、
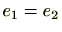
。
(2)
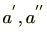
が

の逆元とすると、逆元の定義より
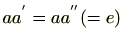
。左より
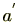
をかけると
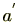
は

の逆元なので、
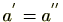
。
(3)
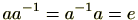
ですが、これは
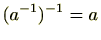
を意味する。
(4)
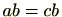
であるとき右から
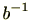
をかけることにより
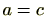
が成り立つ。後者も同様。
群 の元
の元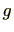 に対し、
に対し、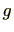 を
を 回かけたもの
回かけたもの
 を
を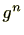 と記載します。また同様に、
と記載します。また同様に、
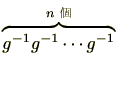 を
を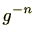 と記載します。すると、通常の指数法則と同様に負の整数を含む整数
と記載します。すると、通常の指数法則と同様に負の整数を含む整数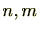 に対し
に対し
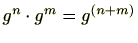 が成り立ちます。
が成り立ちます。
なお、
定義 3.1.4 (アーベル群)
群

の任意の元
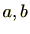
に対し、交換法則すなわち
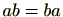
がなりたつとき

を
アーベル群(abelian group)または
可換群(commutative group)という。
一般の群については交換法則は成り立つとは限りません。この定義のようにが、交換法則が成立する群のことをアーベル群といいます。アーベル群の場合、例えば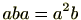 が成りたちます。このように、アーベル群の場合、右からかけるのか左からかけるのかを意識する必要はありません。この意味でアーベル群はとても扱いやすい群だといえます。
が成りたちます。このように、アーベル群の場合、右からかけるのか左からかけるのかを意識する必要はありません。この意味でアーベル群はとても扱いやすい群だといえます。
例 3.1.5 (加法群)
有理数
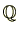
や整数

は加法
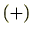
に関し群となります。これを確かめてみましょう。
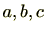
を有理数(又は整数)とします。
すると、
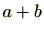
も有理数(又は整数)ですので、有理数(又は整数)は演算(
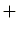
)で閉じています。(条件0)
結合法則
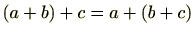
も成り立ちます。(条件1)
また、
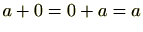
ですので単位元
0が存在します。(条件2)
最後に逆元ですが、
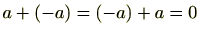
ですので

の逆元は
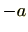
でありこれは常に存在します。(条件3)
このように加法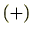 を演算とする群を加法群(additive group)といいます。上の例のとおり加法群の単位元は0であり、
を演算とする群を加法群(additive group)といいます。上の例のとおり加法群の単位元は0であり、 の逆元は
の逆元は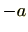 です。
です。
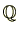 や
や
 には加法とともに乗法も定義されていますので、加法群を考える場合演算記号の
には加法とともに乗法も定義されていますので、加法群を考える場合演算記号の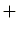 は省略しません。加法群の場合、
は省略しません。加法群の場合、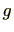 を
を 回足したものは、
回足したものは、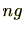 と記載します。(これに対し、加法群以外の群では
と記載します。(これに対し、加法群以外の群では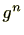 と記載します。)
と記載します。)
例 3.1.6
有理数
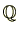
や整数

は乗法(
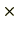
)に関しては全ての元に対し逆元が存在するわけではありませんので、乗法に関しては群になりません。これに対し、
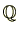
は
0以外の元に対し逆元が存在しますので、
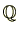
から0を除いた集合
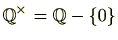
は乗法を演算とする群となります。これを確かめてみましょう。
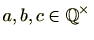
つまり
0以外の有理数とします。
すると、
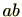
は
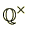
に含まれますので演算は閉じています。(条件0)
また、
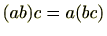
ですので結合法則も成り立ちます。(条件1)
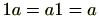
ですので単位元
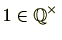
が存在します。(条件2)
最後に、
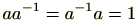
ですので

の逆元
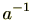
が常に存在します。(条件3)
よって、
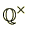
は乗法に関し群となることが分かりました。
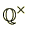 のように乗法に関する群を乗法群といいます。
加法群、乗法群ともにアーベル群です。
のように乗法に関する群を乗法群といいます。
加法群、乗法群ともにアーベル群です。
Remark 3.1.7
一般的に

は加法(
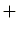
)に関し群となります。そしてこの群を環

の加法群といいます。
また、環

のからなる集合
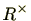
は乗法(
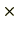
)に関し群をなします。
Takashi
平成24年5月27日
![]() は、
は、
![]() の演算の順序を気にする必要が無いことを意味しています。したがって、3つ以上の演算を考える場合でも
の演算の順序を気にする必要が無いことを意味しています。したがって、3つ以上の演算を考える場合でも
![]() のように括弧をつける必要はありません。結合法則は、演算を考える際には最も基本的な性質です。
のように括弧をつける必要はありません。結合法則は、演算を考える際には最も基本的な性質です。
![]() を考える際の演算は1つに固定されますので特に演算記号を強調する必要がないときは演算記号
を考える際の演算は1つに固定されますので特に演算記号を強調する必要がないときは演算記号![]() を省略し、
を省略し、![]() のことを
のことを![]() と記載します。また、
と記載します。また、![]() と
と![]() の演算をとり
の演算をとり![]() とすることを
とすることを![]() に
に![]() を右からかけるまたは
を右からかけるまたは![]() に
に![]() を左からかけるといいます。「かける」という用語を使っています、自然数などに定義されている「乗法」とは限りません。
を左からかけるといいます。「かける」という用語を使っています、自然数などに定義されている「乗法」とは限りません。
![]() は成り立つとは限りませんので、例えば、
は成り立つとは限りませんので、例えば、![]() と
と![]() は異なるかもしれません。したがって、
は異なるかもしれません。したがって、![]() に
に![]() をかけるというのときに、左から
をかけるというのときに、左から![]() をかけると右から
をかけると右から![]() をかけるとでは結果が異なる場合があります。したがって、単に
をかけるとでは結果が異なる場合があります。したがって、単に![]() をかけるというのは意味がなく、右からかけるのか左からかけるのか明確にする必要があります。
をかけるというのは意味がなく、右からかけるのか左からかけるのか明確にする必要があります。
![]() が群であるとき、演算が定義されていますので、
が群であるとき、演算が定義されていますので、![]() に対し
に対し
![]() です。これを0番目の条件と考えると、集合
です。これを0番目の条件と考えると、集合![]() が群であるときは(0)から(3)までの4つの条件を満たす必要があります。以下で
が群であるときは(0)から(3)までの4つの条件を満たす必要があります。以下で![]() が群であることを確かめるとき、(条件0)から(条件4)を満たしていることを確かめていきます。ある集合が群となるには、この4つの条件を満たす必要があることはよく頭に入れておきましょう。
が群であることを確かめるとき、(条件0)から(条件4)を満たしていることを確かめていきます。ある集合が群となるには、この4つの条件を満たす必要があることはよく頭に入れておきましょう。
![]() の元
の元![]() に対し、
に対し、![]() を
を![]() 回かけたもの
回かけたもの
 を
を![]() と記載します。また同様に、
と記載します。また同様に、
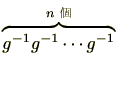 を
を![]() と記載します。すると、通常の指数法則と同様に負の整数を含む整数
と記載します。すると、通常の指数法則と同様に負の整数を含む整数![]() に対し
に対し
![]() が成り立ちます。
が成り立ちます。
![]() が成りたちます。このように、アーベル群の場合、右からかけるのか左からかけるのかを意識する必要はありません。この意味でアーベル群はとても扱いやすい群だといえます。
が成りたちます。このように、アーベル群の場合、右からかけるのか左からかけるのかを意識する必要はありません。この意味でアーベル群はとても扱いやすい群だといえます。
![]() を演算とする群を加法群(additive group)といいます。上の例のとおり加法群の単位元は0であり、
を演算とする群を加法群(additive group)といいます。上の例のとおり加法群の単位元は0であり、![]() の逆元は
の逆元は![]() です。
です。
![]() や
や
![]() には加法とともに乗法も定義されていますので、加法群を考える場合演算記号の
には加法とともに乗法も定義されていますので、加法群を考える場合演算記号の![]() は省略しません。加法群の場合、
は省略しません。加法群の場合、![]() を
を![]() 回足したものは、
回足したものは、![]() と記載します。(これに対し、加法群以外の群では
と記載します。(これに対し、加法群以外の群では![]() と記載します。)
と記載します。)
![]() のように乗法に関する群を乗法群といいます。
加法群、乗法群ともにアーベル群です。
のように乗法に関する群を乗法群といいます。
加法群、乗法群ともにアーベル群です。