Next: 3.1.11 対称群 Up: 3.1 群 Previous: 3.1.9 準同型定理
有限群の重要な例として置換群があります。置換群はガロア理論を学ぶ上で必須のものです。この項では置換群をみていきましょう。
要素が![]() 個ある集合
個ある集合![]() を考えます。
を考えます。![]() は要素の個数が
は要素の個数が![]() であればどのようなものでも構いませんが、ここでは、分かりやすさの観点から
であればどのようなものでも構いませんが、ここでは、分かりやすさの観点から
![]() とおきましょう。
とおきましょう。![]() か
か![]() への全単写のことを
への全単写のことを![]() 次の置換(permutation)といいます。
置換
次の置換(permutation)といいます。
置換![]() は、
は、![]() から
から![]() への全単写ですので、
への全単写ですので、![]() を
を![]() に写し、
に写し、![]() を
を![]() に写し
に写し![]() 、
、![]() を
を![]() に写します。このとき、
に写します。このとき、![]() を記号で
を記号で

置換![]() は、全単射ですので、
は、全単射ですので、
![]() は、
は、![]() から
から![]() までの全ての数字が1回だけ必ず出てきます。
までの全ての数字が1回だけ必ず出てきます。
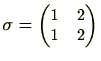 です。
です。
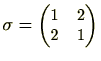 です。
です。
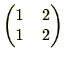 と
と
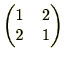 の2つがあります。
の2つがあります。
![]() の恒等写像
の恒等写像
![]() は
は![]() の全単射ですので置換になります。
の全単射ですので置換になります。
![]() のことを恒等置換とよび単に
のことを恒等置換とよび単に
![]() と記載します。また、
と記載します。また、![]() の2元のみを交互に入れ替える置換のことを互換(transposition)といいます。
の2元のみを交互に入れ替える置換のことを互換(transposition)といいます。![]() の2元を
の2元を![]() とすると
とすると![]() を
を![]() に写し、
に写し、![]() を
を![]() に写し、
に写し、![]() 以外はそのままとする写像のことです。
以外はそのままとする写像のことです。![]() を入れ替える互換を
を入れ替える互換を![]() という記号で表します。
という記号で表します。
また、![]() の複数個の元を順繰りに置き換える置換を巡回置換(cycle)といいます(次の例を参照)。互換も巡回置換の1つです。
の複数個の元を順繰りに置き換える置換を巡回置換(cycle)といいます(次の例を参照)。互換も巡回置換の1つです。
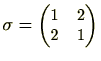 は、1と2を入れ替えていますので互換であり、
は、1と2を入れ替えていますので互換であり、
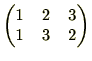 は、2と3を入れ替える互換であり、
は、2と3を入れ替える互換であり、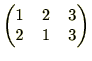 は、
は、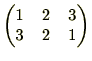 は、
は、
また、
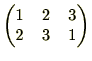 は、
は、
![]() と順繰りに移動させる置換ですので、巡回置換であり
と順繰りに移動させる置換ですので、巡回置換であり![]() と表します。
同様に
と表します。
同様に
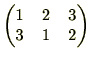 は、
は、![]() と表します。(なお、
と表します。(なお、![]() とも
とも![]() とも記載できますがこれらは全て同じ置換です。)
とも記載できますがこれらは全て同じ置換です。)
このように、2次置換の2つは、
![]() と表され、3次の置換6つは、
と表され、3次の置換6つは、
![]() と表され、これらはすべて巡回置換です(
と表され、これらはすべて巡回置換です(
![]() も
も![]() の0個の元の巡回置換と考えられます。)。一方、
の0個の元の巡回置換と考えられます。)。一方、![]() のときは全ての置換が巡回置換となるわけではありません。
のときは全ての置換が巡回置換となるわけではありません。
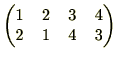 は、巡回置換ではありません。
は、巡回置換ではありません。
Takashi