Next: 3.2 環 Up: 3.1 群 Previous: 3.1.10 置換
![]() 次の置換
次の置換
![]() は、
は、![]() から
から![]() への写像であるため、合成
への写像であるため、合成
![]() を考えることができ、合成も
を考えることができ、合成も![]() から
から![]() への写像となります。また、
への写像となります。また、
![]() は全単写であるためその合成も全単写となります。よって、置換の合成も
は全単写であるためその合成も全単写となります。よって、置換の合成も![]() 次の置換となります。置換の合成では
次の置換となります。置換の合成では![]() を省略し
を省略し
![]() と記載します。
と記載します。
この例のように互換![]() は
は![]() を互いに入れ替えるますので、同じ互換を合成すると元に戻りますので、
を互いに入れ替えるますので、同じ互換を合成すると元に戻りますので、
![]() です。
です。
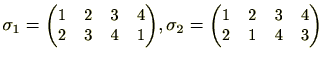 とし、
とし、
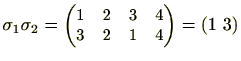
同様に、
![]() を考えてみましょう。今度は、
を考えてみましょう。今度は、![]() が先に作用します。すると、
が先に作用します。すると、
![]() なので
なので![]() を
を![]() に移し、
に移し、
![]() なので
なので![]() を
を![]() に移し、
に移し、
![]() なので
なので![]() を
を![]() に移し、
に移し、
![]() なので
なので![]() を
を![]() に移します。よって、
に移します。よって、
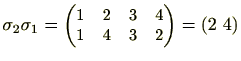
このように、
![]() と
と
![]() は一般的には異なります。
は一般的には異なります。
![]() は上記例のとおり一般的にはアーベル群ではありません。対称群はアーベル群ではない有限群の中ではもっとも基本的な群です。
は上記例のとおり一般的にはアーベル群ではありません。対称群はアーベル群ではない有限群の中ではもっとも基本的な群です。
上の証明では順列
![]() を使いましたが、順列になじみがない場合は、次のように考えることでも分かります。
を使いましたが、順列になじみがない場合は、次のように考えることでも分かります。
![]() 次の置換
次の置換![]() は
は![]() から
から![]() までの像、つまり
までの像、つまり![]() から
から![]() を特定することにより決まりますが、これを順にかんがえてみると、
を特定することにより決まりますが、これを順にかんがえてみると、![]() は
は![]() から
から![]() までの
までの![]() 個が考えられ、
個が考えられ、![]() が特定されると、
が特定されると、![]() は1から
は1から![]() までのうち
までのうち![]() 以外の
以外の![]() 個が、
個が、
![]() が特定されると
が特定されると![]() は1から
は1から![]() までのうちの、
までのうちの、
![]() 以外の
以外の![]() 個に特定され
個に特定され![]() これを繰り返すことにより、全部で
これを繰り返すことにより、全部で![]() 個と分かります。
個と分かります。
![]() が小さいときの群構造をみていきましょう。
が小さいときの群構造をみていきましょう。
また、![]() と
と![]() 以外の元は、
以外の元は、
![]() と表されます。このように
と表されます。このように![]() と
と![]() によって
によって![]() の全ての元が表せるような場合、
の全ての元が表せるような場合、![]() は
は
![]() によって生成されるといいます。そして、
によって生成されるといいます。そして、
![]() ですので
ですので
![]() となります。
となります。
詳細は触れませんが、![]() における群構造は、
における群構造は、
![]() で生成され、
で生成され、![]() と
と![]() の間に
の間に
![]() という関係があることによってすべて分かります。このような関係のことを基本関係と呼びます。
という関係があることによってすべて分かります。このような関係のことを基本関係と呼びます。
![]() ですので
ですので![]() は非可換群です。また、
は非可換群です。また、![]() の元は
の元は![]() の
の![]() の元と考えることができます(4以上の数は恒等置換であると考えることにより)ので、
の元と考えることができます(4以上の数は恒等置換であると考えることにより)ので、![]() の
の![]() に対し
に対し![]() は非可換群であることが分かります。
は非可換群であることが分かります。
Takashi