2つの群の間の準同型写像が定義され、また、2つの群の間の同型が定義されたように環の準同型・同型が定義できます。
定義 3.2.13
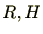
を2つの環とする。
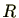
から
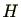
への写像
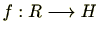
が任意の
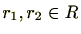
に対し次の条件を満たすとき、
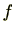
は
準同型写像(homomorphism)であるという。
(1)
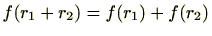
(2)
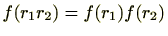
(3)
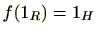
条件(1)(2)は、環の演算(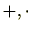 )が写像
)が写像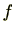 によって保たれていることを意味します。また、環の元は乗法に関する逆元が存在するとは限らないため条件(3)が必要となります。
によって保たれていることを意味します。また、環の元は乗法に関する逆元が存在するとは限らないため条件(3)が必要となります。
群と同様、準同型定理が成り立ちます。
命題 3.2.14
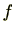
を環
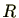
から環
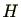
への準同型写像とする。このとき、
(1)
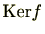
は
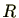
のイデアルとなる。
(2)
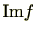
は
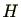
の演算により環となる。
定理 3.2.15 (準同型定理)
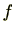
を環
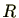
から環
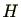
への準同型写像とする。準同型写像
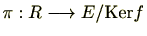
及び
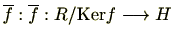
に対し
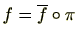
が成り立つ。つまり、次が可換図式となる。
また
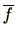
を
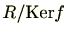
から
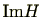
への写像と考えると同型写像となる。
Takashi
平成24年5月27日
![]() )が写像
)が写像![]() によって保たれていることを意味します。また、環の元は乗法に関する逆元が存在するとは限らないため条件(3)が必要となります。
によって保たれていることを意味します。また、環の元は乗法に関する逆元が存在するとは限らないため条件(3)が必要となります。