3.3.1 体
次に体を定義しましょう。下記のように乗法について逆元が存在する可換環を体といいます。体の典型例は、有理数体
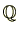 、実数体
、実数体
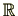 、複素数体
、複素数体
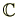 などです。
などです。
定義 3.3.1
集合
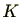
に加法(
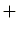
)及び乗法(
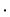
)という2つの演算が定義されており、
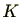
の演算が
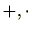
が次の条件を満たす場合集合
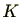
を
体(field)という。
(1)(環であること)
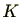
が演算(
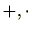
)について
環(このHPでは、単位元を有する可換環)である。
(2)(乗法に関する逆元の存在)
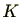
の
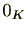
以外の任意の元

に対し、
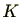
の元
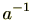
が存在し
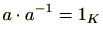
となる。
Remark 3.3.2
上記のとおり体は乗法に関しの交換法則が成り立つ必要がありますが(つまり乗法に関し可換)、文脈によっては交換法則を要件としていない場合があります。また、非可換な体を斜体(skew field)又は非可換体(non-commutative field)といいます。
体である場合には、可換環の要件も満たしますので、体は常に可換環です。例えば、有理数体は体でもあり、環でもあります。
体と環の違いの1つに零因子の存在があります。零因子(zero divisor)とは零元以外の元と乗算することにより零元となる元のことです。
環には逆元が存在しない場合があるため零因子が存在することがあります。例えば、(非可換環ですが)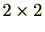 行列では、
行列では、
のように零元以外をかけることにより、零元になることがあります。
また、可換環の例としては、合成数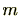 に対する剰余環
に対する剰余環
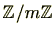 は零因子を持っています。
は零因子を持っています。
しかし、体には零元が存在しません。なぜなら、体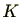 の零元でない元
の零元でない元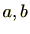 に対し
に対し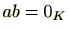 と仮定すると、逆元
と仮定すると、逆元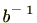 (零元でないので逆元が存在します)をかけると、
(零元でないので逆元が存在します)をかけると、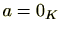 となり、これは仮定に矛盾します。したがって次の命題が成り立ちます。
となり、これは仮定に矛盾します。したがって次の命題が成り立ちます。
命題 3.3.3
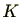
を体とするとき、零元
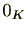
以外の元

は零因子でない。
例 3.3.4
有理数全体
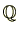
、実数全体
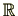
、複素数全体
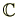
は体となります。
これに対し、整数全体

は体ではありません。
例 3.3.5
合同類には自然な演算(
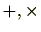
)が定義されこれにより環になります。また、素数を法とする
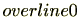
でない合同類には
逆元が存在するので、
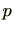
を素数とするとき
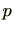
を法とする合同類
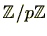
は体となります。
なお、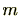 を合成数とすると
を合成数とすると
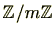 は体にはなりません。
は体にはなりません。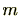 が合成数ですので
が合成数ですので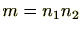 と分解でき
と分解でき
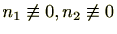 ですが、このとき
ですが、このとき
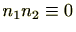 となり、
となり、
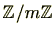 には、必ず零因子
には、必ず零因子
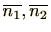 が存在します。一方、体には零因子は存在しないからです。
が存在します。一方、体には零因子は存在しないからです。
以上より、
Takashi
平成24年5月27日
![]() 、実数体
、実数体
![]() 、複素数体
、複素数体
![]() などです。
などです。
![]() 行列では、
行列では、
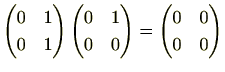
![]() の零元でない元
の零元でない元![]() に対し
に対し![]() と仮定すると、逆元
と仮定すると、逆元![]() (零元でないので逆元が存在します)をかけると、
(零元でないので逆元が存在します)をかけると、![]() となり、これは仮定に矛盾します。したがって次の命題が成り立ちます。
となり、これは仮定に矛盾します。したがって次の命題が成り立ちます。