定義 3.2.1
集合

に加法(
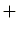
)及び乗法(
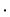
)という2つの演算が定義されており、

の演算が(
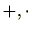
)が次の条件を満たす場合、集合

を
環(Ring)という。
(1) (加法に関する結合法則)

の任意の元
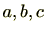
に対し
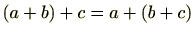
が成り立つ。
(2)(加法に関する交換法則)

の任意の元
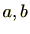
に対し
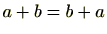
が成り立つ。
(3) (零元の存在)零元とよばれる特殊な元
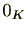
が存在し、

の任意の元

に対し、
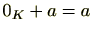
となる
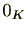
は混同するおそれがないときは単に
0と記載する。
(4) (加法に関する逆元の存在)

の任意の元

に対し、マイナス元
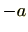
が存在し
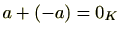
となる。
(5)(乗法に関する結合法則)

の任意の元
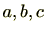
に対し
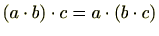
が成り立つ。
(6) (乗法に関する交換法則)

の任意の元
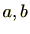
に対し、交換法則
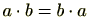
が成り立つ。
(7) (単位元の存在)単位元とよばれる特殊な元
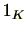
が存在し、

の任意の元

に対し、
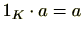
となる。
(8)(分配法則)

の任意の元
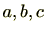
に対し、分配法則
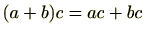
,
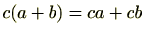
が成り立つ。
条件(1)から(4)は、集合 が加法に関しアーベル群であることと同値です。また、環
が加法に関しアーベル群であることと同値です。また、環 は乗法に関しては群になるとは限りません。
は乗法に関しては群になるとは限りません。
環 の元には加法に関する逆元が存在するため、
の元には加法に関する逆元が存在するため、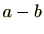 を
を
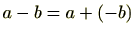 と定義することにより減法も定義できます。すなわち、環
と定義することにより減法も定義できます。すなわち、環 には加減乗の3つの算法が定義されていることになります。しかし、除法は加法及び加法に関する逆元の存在から定義できますので本質的には2つの演算が定義されているにすぎません。
には加減乗の3つの算法が定義されていることになります。しかし、除法は加法及び加法に関する逆元の存在から定義できますので本質的には2つの演算が定義されているにすぎません。
このように、環には(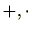 )の2つの演算が定義されており、その2つの演算は分配法則で関連しています。このHPでは乗法に関しては交換法則を条件(6)としています。このように、交換法則
)の2つの演算が定義されており、その2つの演算は分配法則で関連しています。このHPでは乗法に関しては交換法則を条件(6)としています。このように、交換法則
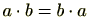 が成り立つような
が成り立つような を特に可換環(commutative ring)ということがあります。一般的には、可換でない環(非可換環)も環という場合があります。
を特に可換環(commutative ring)ということがあります。一般的には、可換でない環(非可換環)も環という場合があります。
下記の例のとおり、可換環の典型例としては整数環や多項式環が、非可換環の典型例としては行列環があります。
本HPでは、単に環という場合、可換環を意味することに注意しましょう。
例 3.2.2
整数全体からなる集合

には(
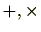
)という2つの演算が定義されており、この演算に関し整数全体

は環になります。整数環は乗法に関し交換法則が成り立っていますので可換環です。整数は乗法に関する逆元が存在しないことに注意しましょう。
同様に、有理数全体からなる集合
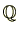
、実数全体からなる集合
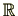
、複素数全体からなる集合
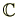
には演算(
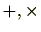
)が定義されておりこれらこの演算に関し環になります。また、乗法に関し交換法則が成り立ちますのでこれらはすべて可換環になります。
他方、自然数全体からなる集合
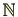
や0以上の整数全体からなる集合
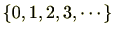
は環ではありません。(加法に関する逆元
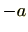
が定義できないからです。)
Remark 3.2.3
次項のとおり
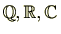
は体です。一般的に体は環ですが、環は体ではありません。
例 3.2.4
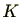
を環とすると
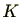
を係数とする
多項式全体の集合
![$ K[\mathrm{X}]$](numbertheory-img1619.png)
は環となります。
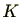
が可換環であるとき
![$ K[\mathrm{X}]$](numbertheory-img1619.png)
も可換環です。
例 3.2.5
非可換環の例として
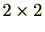
行列全体からなる集合
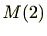
があります。
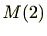
には自然な演算が定義されていますが、この自然な演算に対し環になります。しかし、
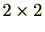
行列
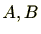
に対し
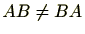
ですので可換環ではありません。(このような環を非可換環ということがあります。)
例 3.2.6
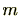
を自然数とするとき
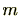
を法とする
合同類
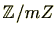
は、合同類に自然に定義される
演算により可換環になります。
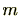 が素数のときは体となります。
が素数のときは体となります。
定義 3.2.7
環

の元
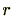
が乗法に関する逆元をもつとき(つまり、
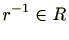
のとき)、
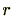
を
可逆元(invertible element)という。

の可逆元全体からなる集合を

の
乗法群(multiplicative group)といい、
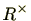
と記載する。
命題 3.2.8
環

の乗法群
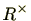
は群となる。
例 3.2.9
整数環

の乗法群は
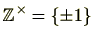
です。位数2の群は全て
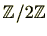
と同型ですので
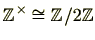
です。
体の
0以外の元は可逆元ですので、
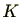
を体と
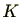
の乗法群は
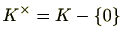
です。したがって、
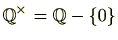
,
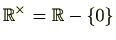
,
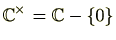
です。
また、多項式環
![$ K[X]$](numbertheory-img1641.png)
の乗法群
![$ (K[X])^{\times}$](numbertheory-img1642.png)
は
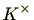
です。
Takashi
平成24年5月27日
![]() が加法に関しアーベル群であることと同値です。また、環
が加法に関しアーベル群であることと同値です。また、環![]() は乗法に関しては群になるとは限りません。
は乗法に関しては群になるとは限りません。
![]() の元には加法に関する逆元が存在するため、
の元には加法に関する逆元が存在するため、![]() を
を
![]() と定義することにより減法も定義できます。すなわち、環
と定義することにより減法も定義できます。すなわち、環![]() には加減乗の3つの算法が定義されていることになります。しかし、除法は加法及び加法に関する逆元の存在から定義できますので本質的には2つの演算が定義されているにすぎません。
には加減乗の3つの算法が定義されていることになります。しかし、除法は加法及び加法に関する逆元の存在から定義できますので本質的には2つの演算が定義されているにすぎません。
![]() )の2つの演算が定義されており、その2つの演算は分配法則で関連しています。このHPでは乗法に関しては交換法則を条件(6)としています。このように、交換法則
)の2つの演算が定義されており、その2つの演算は分配法則で関連しています。このHPでは乗法に関しては交換法則を条件(6)としています。このように、交換法則
![]() が成り立つような
が成り立つような![]() を特に可換環(commutative ring)ということがあります。一般的には、可換でない環(非可換環)も環という場合があります。
を特に可換環(commutative ring)ということがあります。一般的には、可換でない環(非可換環)も環という場合があります。