2.2.6 多項式環のイデアル
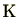 を
を
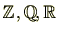 または
または
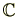 とします。(この項では、
とします。(この項では、
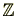 も許容されることに留意。)
も許容されることに留意。)
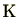 係数多項式全体からなる集合
係数多項式全体からなる集合
![$ \mathrm{K}[\mathrm{X}]$](numbertheory-img490.png) は可換環となるため、定義2.1.20と同様に
は可換環となるため、定義2.1.20と同様に
![$ \mathrm{K}[\mathrm{X}]$](numbertheory-img490.png) のイデアルが定義できます。
のイデアルが定義できます。
定義 2.2.17
![$ \mathrm{K}[\mathrm{X}]$](numbertheory-img490.png)
の部分集合
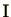
で次の性質を持つものを
![$ \mathrm{K}[\mathrm{X}]$](numbertheory-img490.png)
の
イデアル(ideal)であるという。
-
![$ f\in {\mathrm I},g\in \mathrm{K}[\mathrm{X}]\Rightarrow gf\in {\mathrm I}$](numbertheory-img565.png)
-
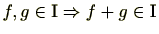
整数のイデアルと同様に
![$ f_1,f_2,\cdots,f_k\in \mathrm{K}[\mathrm{X}]$](numbertheory-img567.png) に対し、
に対し、
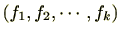 を、
を、
と定義します。
すると、整数イデアルに関する場合と同様に、
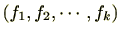 はイデアルになります。
はイデアルになります。
そして、整数イデアルの場合と同様に、有限生成イデアル、単項イデアルが定義され次の定理がなりたちます。
定理 2.2.18
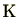
を
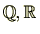
または
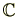
とする。
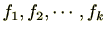
の最大公約式を
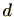
とすると、
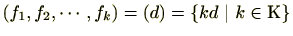
また、
![$ \mathrm{K}[\mathrm{X}]$](numbertheory-img490.png)
の任意のイデアル
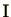
に対し整数
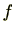
が存在し、
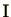
は
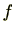
から生成される。この場合、
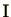
の生成元は
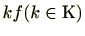
に限る。
Takashi
平成24年5月27日
![]() に対し、
に対し、
![]() を、
を、