2.1.4 整数のイデアル
整数
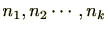 に対し、
に対し、
 の部分集合
の部分集合
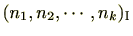 を、
を、
で定義します。
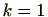 のときは、
のときは、
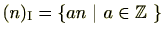 であり
であり の倍数の集合と一致します。
の倍数の集合と一致します。
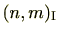 という記号は通常は使いません。通常は、単に
という記号は通常は使いません。通常は、単に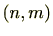 と記載しますが、
と記載しますが、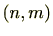 は最大公約数を意味していますので、
は最大公約数を意味していますので、
 の部分集合である
の部分集合である
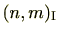 と混乱しないように記号を分けました。しかし、次の定理より
と混乱しないように記号を分けました。しかし、次の定理より
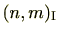 と最大公約数
と最大公約数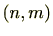 は実質的に同じものであることが分かりますので、
は実質的に同じものであることが分かりますので、
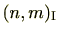 の代わりに
の代わりに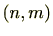 と記載しても混同する心配はほとんどありません。
と記載しても混同する心配はほとんどありません。
定理 2.1.19
整数
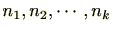
に対し、
(1)
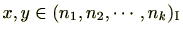
のとき、
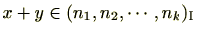
(2)
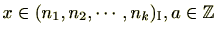
のとき、
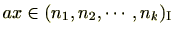
(3)
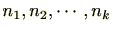
の最大公約数を
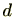
とすると、
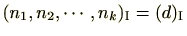
(4) 仮に

であった場合、
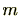
は
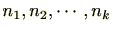
の最大公約数又は最大公約数を負にしたものである。
証明
(1)
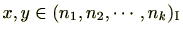
とすると、
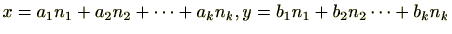
となる
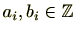
が存在する。すると、
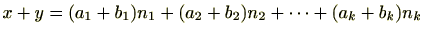
であり、
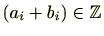
ですので、
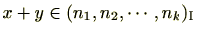
(2) また、
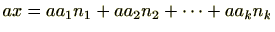
であり
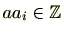
ですので、
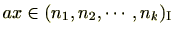
(3)
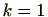
のときは明らか。
また、
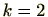
のときは
定理2.1.17より成立している。
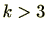
のときは数学的帰納法を用いて証明することもできますし、
定理2.1.17が3つ以上の整数に対しても成立していることからも分かります。
(4)
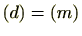
とすると、定義より、
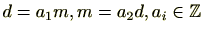
であるが、このようなことが成立するのは、
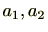
が
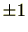
のときに限る。よって、証明された。
つぎに
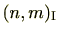 を一般化したイデアルを定義しましょう。
を一般化したイデアルを定義しましょう。
 のイデアルは
のイデアルは
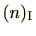 形をしていることが分かります。
形をしていることが分かります。
定義 2.1.20

の部分集合
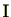
で次の性質を持つものを

の
イデアル(ideal)であるという。
(1)
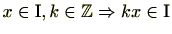
(2)
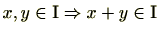
定義の(1)は
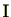 を整数倍しても
を整数倍しても
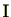 に含まれることを意味しています。また、(2)は
に含まれることを意味しています。また、(2)は
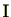 が加法について閉じていることを意味しています。
(1)により、必ず0は
が加法について閉じていることを意味しています。
(1)により、必ず0は
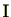 に含まれることが分かります。また、仮に
に含まれることが分かります。また、仮に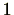 が
が
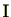 に含まれていると仮定すると
に含まれていると仮定すると
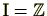 となります。
となります。
Remark 2.1.21
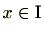
に対し定義(1)より
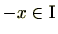
と分かります。定義(2)と考え合わせると、

を
加法群と考える場合
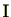
は

の
部分群になります。逆に、

を加法群と考えるときの

の部分群はイデアルになります。
このように、
 の部分群と
の部分群と
 のイデアルは同じものになります。しかし、一般的に環のイデアルは環の部分集合として定義されますが、環の加法群の部分群が環のイデアルになるとは限りません。
のイデアルは同じものになります。しかし、一般的に環のイデアルは環の部分集合として定義されますが、環の加法群の部分群が環のイデアルになるとは限りません。
例 2.1.22

の部分集合
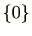
は
定義2.1.20を満たしますのでイデアルです。
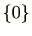
を
零イデアルといいます。

自身も

の部分集合であり、
定義2.1.20を満たしますのでイデアルです。
これらを

の
自明なイデアルといいます。
定義 2.1.24
イデアル
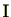
が
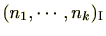
と一致する場合、イデアル
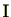
は、
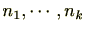 から生成される(generated)
から生成される(generated)といい、
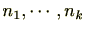
をイデアル
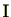
の
生成元(generator)であるという。有限個の生成元から生成されるイデアルを
有限生成イデアル(finitely generated ideal)、1つ元から生成されるイデアルを
単項イデアル(principal ideal)という。
例 2.1.25

の自明なイデアルである

は、
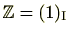
ですので単項イデアルです。
同様に、零イデアル
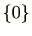
は
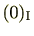
ですので単項イデアルです。
定理2.1.19により、
 における有限生成イデアルは、単項イデアルであることが分かります。次の定理は、
における有限生成イデアルは、単項イデアルであることが分かります。次の定理は、
 の全てのイデアルが単項イデアルであることを示しています。
の全てのイデアルが単項イデアルであることを示しています。
定理 2.1.26

のイデアル
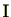
に対し整数

が存在し、
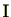
は

から生成される。この場合、
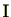
の生成元は
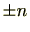
に限る。
証明
零イデアル
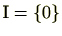
の場合は明らか。零イデアル以外のイデアル
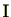
には必ず正の元が含まれている。(
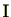
の元を
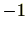
倍しても
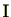
に含まれるため。)
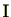
の正の元でもっとも小さい元を

とするとき、
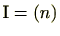
であることを以下証明する。
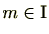
とし、

と
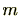
の最大公約数を
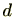
とすると
定理2.1.17より
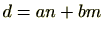
となる整数
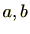
が存在しますが、イデアルの定義より
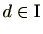
となります。
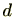
は最大公約数であるため

以下であり、他方、

は最小数であるため
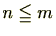
。したがって
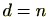
。よって、

と
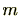
の最大公約数が
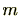
であり、これは

が
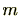
の倍数であることを意味する。よって、
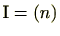
であることが証明された。
後段は、
定理2.1.19により証明されている。
Remark 2.1.27
一般論として、イデアルは環において定義されます。イデアルは常に有限生成とは限りませんし、有限生成イデアルが単項イデアルになるわけでもありません。
しかし、ユークリッド整域においては、全てのイデアルは単項イデアルになります。
例 2.1.28
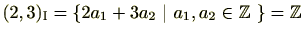
以上のとおり、
 のイデアルは常に有限生成であり、また、生成元は最大公約数になることがわかります。つまり、
のイデアルは常に有限生成であり、また、生成元は最大公約数になることがわかります。つまり、
です。ここで、
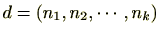 です。このように、イデアル
です。このように、イデアル
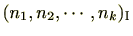 と最大公約数
と最大公約数
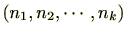 は同視することができるため、通常、イデアルの記号には
は同視することができるため、通常、イデアルの記号には
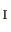 を付さずに単に
を付さずに単に
 と記載します。このように、記載してもこれが最大公約数を意味するのか、最大公約数から生成されるイデアルを意味するのかは、通常、前後の文脈から明らかであるため特に混乱することはありません。
と記載します。このように、記載してもこれが最大公約数を意味するのか、最大公約数から生成されるイデアルを意味するのかは、通常、前後の文脈から明らかであるため特に混乱することはありません。
Takashi
平成24年5月27日
![]() に対し、
に対し、
![]() の部分集合
の部分集合
![]() を、
を、
![]() のときは、
のときは、
![]() であり
であり![]() の倍数の集合と一致します。
の倍数の集合と一致します。
![]() という記号は通常は使いません。通常は、単に
という記号は通常は使いません。通常は、単に![]() と記載しますが、
と記載しますが、![]() は最大公約数を意味していますので、
は最大公約数を意味していますので、
![]() の部分集合である
の部分集合である
![]() と混乱しないように記号を分けました。しかし、次の定理より
と混乱しないように記号を分けました。しかし、次の定理より
![]() と最大公約数
と最大公約数![]() は実質的に同じものであることが分かりますので、
は実質的に同じものであることが分かりますので、
![]() の代わりに
の代わりに![]() と記載しても混同する心配はほとんどありません。
と記載しても混同する心配はほとんどありません。
![]() を一般化したイデアルを定義しましょう。
を一般化したイデアルを定義しましょう。
![]() のイデアルは
のイデアルは
![]() 形をしていることが分かります。
形をしていることが分かります。
![]() を整数倍しても
を整数倍しても
![]() に含まれることを意味しています。また、(2)は
に含まれることを意味しています。また、(2)は
![]() が加法について閉じていることを意味しています。
(1)により、必ず0は
が加法について閉じていることを意味しています。
(1)により、必ず0は
![]() に含まれることが分かります。また、仮に
に含まれることが分かります。また、仮に![]() が
が
![]() に含まれていると仮定すると
に含まれていると仮定すると
![]() となります。
となります。
![]() における有限生成イデアルは、単項イデアルであることが分かります。次の定理は、
における有限生成イデアルは、単項イデアルであることが分かります。次の定理は、
![]() の全てのイデアルが単項イデアルであることを示しています。
の全てのイデアルが単項イデアルであることを示しています。
![]() のイデアルは常に有限生成であり、また、生成元は最大公約数になることがわかります。つまり、
のイデアルは常に有限生成であり、また、生成元は最大公約数になることがわかります。つまり、