Next: 2.4 合同式の整数論 Up: 2.3 円分多項式 Previous: 2.3.4 オイラー関数
定理2.3.10より、1の原始![]() 乗根は
乗根は![]() 個あることが分かります。1の原始
個あることが分かります。1の原始![]() 乗根全てを解とする多項式を円分多項式(cyclotomic polynomial)といい、
乗根全てを解とする多項式を円分多項式(cyclotomic polynomial)といい、
![]() で表します。つまり、1の原始
で表します。つまり、1の原始![]() 乗根を、
乗根を、
![]() とすると、円分多項式
とすると、円分多項式
![]() は、
は、
| (2.12) |
円分多項式の具体例を見ていきましょう。
この例から分かるとおり、円分多項式は整数係数多項式になります。また、
![]() 上既約多項式です。証明は、後に行いますがここでは事実のみ定理の形で述べておきます。
上既約多項式です。証明は、後に行いますがここでは事実のみ定理の形で述べておきます。
円分多項式を具体的に求めるのに必要な性質は以下の定理です。円分多項式の性質として通常メビウスの反転公式が掲げられていますが、メビウスの反転公式を用いて円分多項式を求めることはできません。具体的に円分多項式を求める際は下記の性質が重要です。
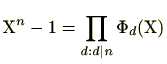
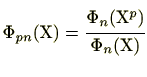
上の命題を使って、少し大きな![]() についての円分多項式の具体例を見ていきましょう。
についての円分多項式の具体例を見ていきましょう。
Takashi