Next: 2.5.2 平方剰余の相互法則 Up: 2.5 平方剰余の相互法則 Previous: 2.5 平方剰余の相互法則
![]() を素数とし、
を素数とし、![]() を
を![]() と素な整数とします。このとき2次方程式
と素な整数とします。このとき2次方程式
素数を法とする合同類には原始根があり、すべての合同類は原始根のべき乗で表すことができます。したがって、![]() を原始根とすると任意の合同類は、
を原始根とすると任意の合同類は、
![]() で表すことができます。
で表すことができます。
![]() が属する剰余類が
が属する剰余類が![]() と表されるとき、
と表されるとき、![]() が偶数の場合、
が偶数の場合、
![]() とすると、
とすると、
![]() となるため、上の式が解を持つことが分かります。
となるため、上の式が解を持つことが分かります。
逆に上の式が解をもつと仮定すると、![]() とおけ、
とおけ、
![]() となるため、
となるため、![]() は原始根の偶数乗であることが分かります。
は原始根の偶数乗であることが分かります。
つまり、上の2次合同式の![]() が原始根の偶数乗のとき、上の合同式は解を持ち、逆に、解を持つときは
が原始根の偶数乗のとき、上の合同式は解を持ち、逆に、解を持つときは![]() が原始根の偶数乗のときに限ります。
が原始根の偶数乗のときに限ります。
この考察は原始根![]() の取り方に依存していないことに注意しましょう。このことは、下記の補題からも確認できます。
の取り方に依存していないことに注意しましょう。このことは、下記の補題からも確認できます。
ここで、ルジャンドル記号
![]() を次のように導入します。
を次のように導入します。
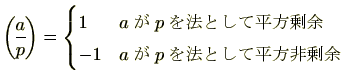 |
フェルマーの小定理より、0以外の合同類は![]() 乗すると
乗すると
![]() になりますが、合同類が原始根の偶数乗と表されるときは
になりますが、合同類が原始根の偶数乗と表されるときは
![]() 乗することにより
乗することにより
![]() となり、原始根の奇数乗と表されるときは
となり、原始根の奇数乗と表されるときは
![]() 乗すると
乗すると
![]() となることが分かります。したがって、ルジャンドル記号は、
となることが分かります。したがって、ルジャンドル記号は、
![]() 乗と等しいことがわかります
以上のルジャンドル記号の性質をまとめると次のようになります。
乗と等しいことがわかります
以上のルジャンドル記号の性質をまとめると次のようになります。
ルジャンドル記号の基本的な性質をみていきましょう。![]() 以外の素数は奇数ですので
以外の素数は奇数ですので![]() でない素数を奇素数(odd prime)といいます。
でない素数を奇素数(odd prime)といいます。
(2)は、
![]() が
が
![]() から
から
![]() への群準同型写像であることを意味しています。つまり、
への群準同型写像であることを意味しています。つまり、
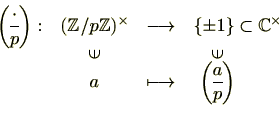
また、(4)の意味するところは以下のとおりです。
2でない素数![]() は、
は、![]() で、1,3,5,7のいずれかです。そして、1,7のとき、
で、1,3,5,7のいずれかです。そして、1,7のとき、
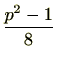 が偶数となり、3,5のとき奇数になりますしたがって(4)を言い換えると次のようになります。
が偶数となり、3,5のとき奇数になりますしたがって(4)を言い換えると次のようになります。
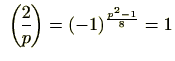 |
|||
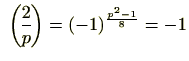 |
Takashi