平方剰余の相互法則の証明をするためにガウス和を導入します。
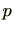 を素数とし、
を素数とし、
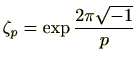 とすると、
とすると、 は1の
は1の 乗根の1つであり、また、
乗根の1つであり、また、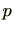 乗してはじめて1になる数です。このように
乗してはじめて1になる数です。このように 乗してはじめて1になる数を原始
乗してはじめて1になる数を原始 乗根(primitive n-th root)といいます。
乗根(primitive n-th root)といいます。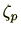 は原始
は原始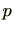 乗根です。
乗根です。
1の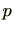 乗根は、原始
乗根は、原始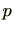 乗根
乗根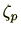 を使って
を使って
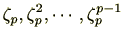 と書けます。
と書けます。
たとえば、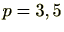 のときは、
のときは、
です。
ここで、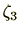 には、
には、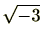 が含まれており、
が含まれており、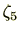 には
には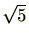 が含まれていいることが分かりますね。
が含まれていいることが分かりますね。
ガウス和とは、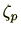 に含まれている
に含まれている
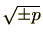 を取りだそうというものです。
を取りだそうというものです。
具体的には、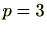 のときは、
のときは、
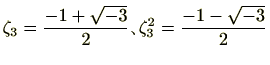 ですので、
ですので、
です。
また、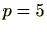 のときは、
のときは、
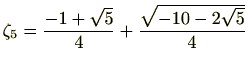 です。詳細は省略しますが、
です。詳細は省略しますが、
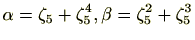 、つまり、
、つまり、
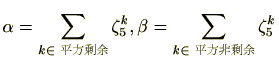 とおくと、
とおくと、
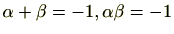 となり、
となり、
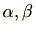 は2次方程式
は2次方程式
の解となることが分かります。
すると、この2次方程式の判別式は、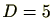 となりますので、
となりますので、
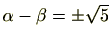 となります。つまり、
となります。(実際には、右辺の符合は+になります。)
となります。つまり、
となります。(実際には、右辺の符合は+になります。)
また、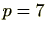 のときは、同様に
のときは、同様に
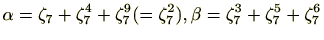 、つまり、
、つまり、
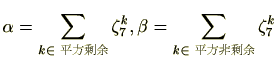 とおくと、
とおくと、
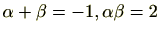 となり、
となり、
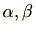 は2次方程式
は2次方程式
の解となることが分かります。すると、この2次方程式の判別式は、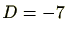 となりますので、
となりますので、
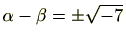 となります。つまり、
となります。(この場合も、実際には、右辺の符合は+です。)
となります。つまり、
となります。(この場合も、実際には、右辺の符合は+です。)
それでは、ガウス和を導入しましょう。
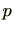 を素数、
を素数、
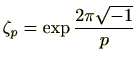 とするとき、ガウス和(Gauss sum)を
とするとき、ガウス和(Gauss sum)を
で定義します。
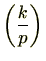 は、ルジャンドル記号です。ルジャンドル記号の定義より、
と変形することができます。また、平方剰余、平方非剰余は、原始根の取り方によりませんので、上記の
は、ルジャンドル記号です。ルジャンドル記号の定義より、
と変形することができます。また、平方剰余、平方非剰余は、原始根の取り方によりませんので、上記の の定義では、原始根として、
の定義では、原始根として、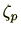 としていますが、これは原始根の取り方に依存しないことに留意しましょう。
としていますが、これは原始根の取り方に依存しないことに留意しましょう。
前項の具体例より、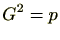 であることが予想されます。本項では
であることが予想されます。本項では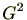 を求めてみましょう。
を求めてみましょう。
そのために、 を整数とするときに
を整数とするときに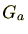 を
を
で定義します。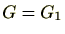 です。
です。
命題 2.5.9

を整数とするとき、
(1)
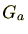
は、
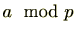
により定まる。
(2)
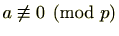
に対し
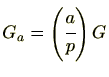
(3)
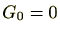
(4)
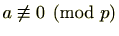
に対し
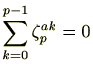
証明
(1)
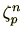
は、
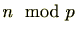
によって定まることより明らか。
(2)
(3)
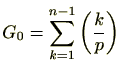
ですが、
命題2.5.3より
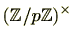
の半分の
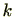
で
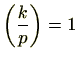
で残りの半分の
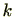
で
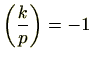
ですので
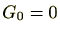
(4)
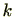
が
0から
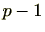
を動くとき
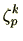
は
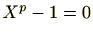
の異なる解となる。したがって、解と係数の関係より
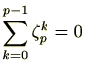
である。
また、
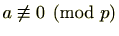
のとき

は

で逆元をもつ(
定理2.4.18)ため、
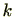
が
0から
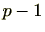
を動くとき
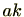
も
0から
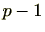
を動く。したがって、
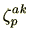
は
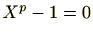
の異なる解となるため、同様に
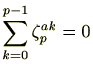
である。
いよいよ本節のメイン定理です。
定理 2.5.10
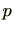
を奇素数とするとき、
証明
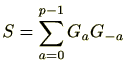
を2種類の方法で計算します。
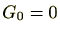
にもかかわらず、左の和は、
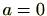
を含める理由は後ほど分かります。
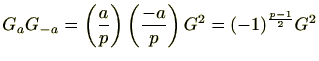
ですので(
第一補充法則)、
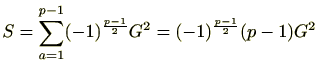
です。
他方、
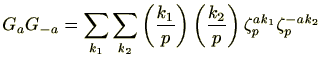
ですので、
です。
この2つの
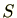
を比較することにより、
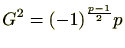
が分かります。
どうですか?不思議な証明ですね。和を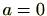 からとった理由は分かりましたか?
からとった理由は分かりましたか?
単独で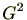 を求めるのは難しいですが、パラメーターを一つ増やした
を求めるのは難しいですが、パラメーターを一つ増やした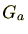 を持ち出し、
を持ち出し、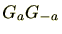 の和を考えるあたり、単独の積分が求められないのに、二重積分が求められる場合と類似しています。
の和を考えるあたり、単独の積分が求められないのに、二重積分が求められる場合と類似しています。
この定理から は、
は、
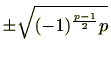 のいずれかであることが分かりますが、前項の例で見たとおり、
のいずれかであることが分かりますが、前項の例で見たとおり、
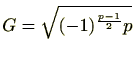 となります。しかし、この証明は簡単ではありません。
となります。しかし、この証明は簡単ではありません。
Remark 2.5.11
最後にこの定理の意味について、考えてみましょう。この定理は、円分多項式
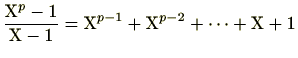
の解
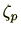
により、
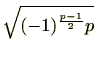
が表せることを意味しています。体の言葉を使うと、有理数体
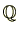
の2次拡大体である
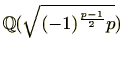
が円分拡大体
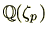
の部分体となっていることを意味します。
Remark 2.5.12
証明は後にしますが、クロネッカー=ウェーバーの定理 (Kronecker-Weber's theorem)を見てみましょう。
定理 2.5.13 (クロネッカー=ウェーバーの定理)
(1)
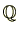
上の任意のアーベル方程式
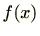
の解は、円分多項式
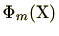
の解の有理式として表せる。
(2)
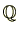
上アーベル拡大体
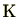
は、円分拡大体
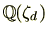
の部分体となる。
ガウス和は、クロネッカー=ウェーバーの定理の簡単な具体例であることが分かります。この、クロネッカー=ウェーバーの定理は、類体論の最も簡単な具体例であることが後に分かります。この意味で、ガウス和は、類体論の最も簡単な場合の更にそのまた簡単な具体例であることが分かります。
Takashi
平成24年5月27日
![]() を素数とし、
を素数とし、
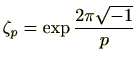 とすると、
とすると、![]() は1の
は1の![]() 乗根の1つであり、また、
乗根の1つであり、また、![]() 乗してはじめて1になる数です。このように
乗してはじめて1になる数です。このように![]() 乗してはじめて1になる数を原始
乗してはじめて1になる数を原始![]() 乗根(primitive n-th root)といいます。
乗根(primitive n-th root)といいます。![]() は原始
は原始![]() 乗根です。
乗根です。
![]() 乗根は、原始
乗根は、原始![]() 乗根
乗根![]() を使って
を使って
![]() と書けます。
と書けます。
![]() のときは、
のときは、
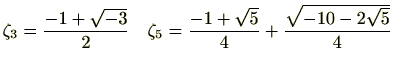
![]() に含まれている
に含まれている
![]() を取りだそうというものです。
を取りだそうというものです。
![]() のときは、
のときは、
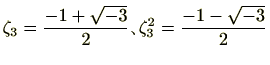 ですので、
ですので、
![]() のときは、
のときは、
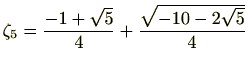 です。詳細は省略しますが、
です。詳細は省略しますが、
![]() 、つまり、
、つまり、
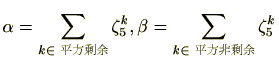 とおくと、
とおくと、
![]() となり、
となり、
![]() は2次方程式
は2次方程式
![]() のときは、同様に
のときは、同様に
![]() 、つまり、
、つまり、
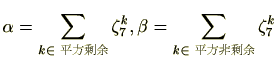 とおくと、
とおくと、
![]() となり、
となり、
![]() は2次方程式
は2次方程式
![]() を素数、
を素数、
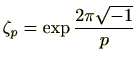 とするとき、ガウス和(Gauss sum)を
とするとき、ガウス和(Gauss sum)を
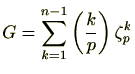
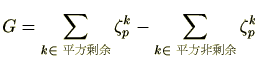
![]() であることが予想されます。本項では
であることが予想されます。本項では![]() を求めてみましょう。
を求めてみましょう。
![]() を整数とするときに
を整数とするときに![]() を
を
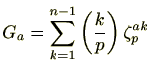
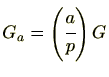
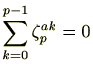
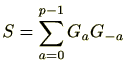 を2種類の方法で計算します。
を2種類の方法で計算します。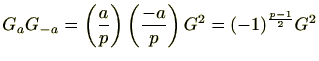 ですので(第一補充法則)、
ですので(第一補充法則)、
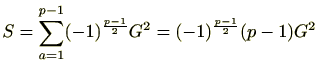 です。
です。
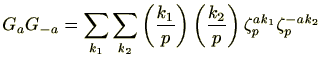 ですので、
ですので、
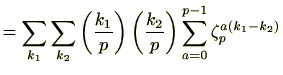
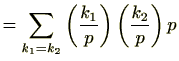
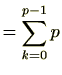
![]() からとった理由は分かりましたか?
からとった理由は分かりましたか?
![]() を求めるのは難しいですが、パラメーターを一つ増やした
を求めるのは難しいですが、パラメーターを一つ増やした![]() を持ち出し、
を持ち出し、![]() の和を考えるあたり、単独の積分が求められないのに、二重積分が求められる場合と類似しています。
の和を考えるあたり、単独の積分が求められないのに、二重積分が求められる場合と類似しています。
![]() は、
は、
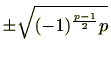 のいずれかであることが分かりますが、前項の例で見たとおり、
のいずれかであることが分かりますが、前項の例で見たとおり、
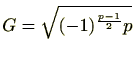 となります。しかし、この証明は簡単ではありません。
となります。しかし、この証明は簡単ではありません。
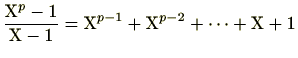 の解
の解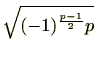 が表せることを意味しています。体の言葉を使うと、有理数体
が表せることを意味しています。体の言葉を使うと、有理数体
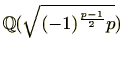 が円分拡大体
が円分拡大体