Next: 2.5 平方剰余の相互法則 Up: 2.4 合同式の整数論 Previous: 2.4.4 中国剰余定理(Chinese remainder theorem)
次の定理は、様々なところで応用される重要な定理です。
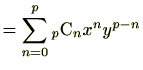 |
||
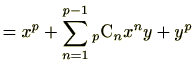 |
||
|
ここで次の補題を用いると第2項は
| ||
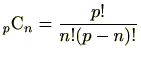 であるが、
であるが、
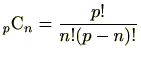 は整数となるが、分子は
は整数となるが、分子はこの定理を使いフェルマーの小定理を証明してみましょう。
この定理から、![]() の零でない合同類は、
の零でない合同類は、![]() 乗すると必ず
乗すると必ず
![]() (1を含む合同類を意味しています。)に等しいことがわかります。更にこれから示すように、
(1を含む合同類を意味しています。)に等しいことがわかります。更にこれから示すように、![]() 乗して初めて
乗して初めて
![]() になる合同類が存在することが分かります。そのような合同類を、pを法とする原始根(primitive root)又は原始元といいます。合同類
になる合同類が存在することが分かります。そのような合同類を、pを法とする原始根(primitive root)又は原始元といいます。合同類
![]() が原始根のとき、整数
が原始根のとき、整数![]() も原始根といいます。
も原始根といいます。![]() を固定している限り、この場合、合同類を考えても整数を考えても意味は一緒だからです。
を固定している限り、この場合、合同類を考えても整数を考えても意味は一緒だからです。
証明は決して難しくありませが、いくつかのステップをたどる必要がありますので、ここでは省略します。
原始根が1つ分かれば命題3.1.14より他の原始根を求めることができます。
この例では6が原始根だと分かりましたので、![]() と互いに素な
と互いに素な![]() に対し
に対し![]() が原始根となります。
が原始根となります。![]() と互いな素な数として1,3,5,7,9,11,13,15(つまり、奇数)がとれます。上の表より原始根は、6,12,7,14,11,5,10,3であることが分かります。
と互いな素な数として1,3,5,7,9,11,13,15(つまり、奇数)がとれます。上の表より原始根は、6,12,7,14,11,5,10,3であることが分かります。
Takashi