3.1.6 剰余類
 を群、
を群、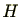 をその部分群とします。このとき、
をその部分群とします。このとき、 の元
の元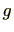 に対し
に対し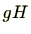 を
を
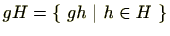 で定義します。つまり、
で定義します。つまり、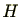 の元に
の元に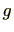 を左からかけた
を左からかけた の部分集合です。同様に
の部分集合です。同様に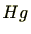 を
を
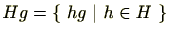 で定義します。このとき、
で定義します。このとき、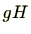 や
や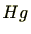 は
は の部分集合ですが、部分群にはなるとは限りません。
の部分集合ですが、部分群にはなるとは限りません。
補題 3.1.26

を群、
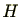
をその部分群とするとき、
証明
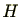
は部分群ですので、
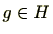
のとき
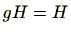
となります。
逆に、
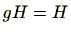
のとき(
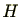
には単位元が含まれますので)
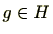
となります。
右側の同値も同様に証明できます。
 を群
を群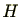 をその部分群とするとき、
をその部分群とするとき、 の2元
の2元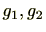 に対し関係
に対し関係
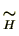 を、
を、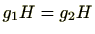 のとき
のとき
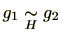 であると定義します。
であると定義します。
補題 3.1.27
(1)

の2元に対する関係
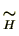
は
同値関係となる。
(2)
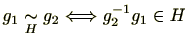
証明
(1)
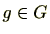
に対し
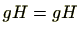
であるため、
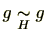
(
反射律)。
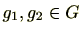
に対し、
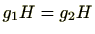
のとき
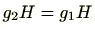
であるため(
対称律)も明らか。
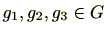
に対し、
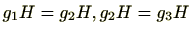
のとき
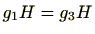
は明らかであるため、
推移律も明らか。
(2)
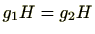
と
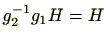
は同値であるため、上の補題により明らか。
群 にはもう1つの関係
にはもう1つの関係
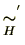 を
を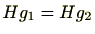 のときに
のときに
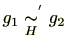 と定義することにより上記と同様に同値関係を定義できます。
と定義することにより上記と同様に同値関係を定義できます。
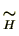 との違いは
との違いは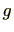 が
が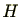 の左側にあるか右側にあるかです。
の左側にあるか右側にあるかです。
同値関係
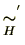 と同値関係
と同値関係
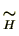 は、一般的には異なります。これが同じ関係になるような部分群
は、一般的には異なります。これが同じ関係になるような部分群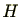 は大変重要です。
は大変重要です。
群 に同値関係が定義されましたので、これに関する同値類が定義できます。
に同値関係が定義されましたので、これに関する同値類が定義できます。
定義 3.1.28
群

その部分群
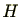
に対し、群

の同値関係
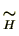
に関する同値類
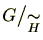
を群

の
右剰余類(right coset)といい、
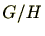
と記載する。
同様に、同値関係
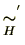
に関する同値類
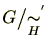
を群

の
左剰余類(left coset)といい、
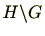
と記載する。
 がアーベル群のとき、
がアーベル群のとき、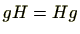 ですので右剰余類と左剰余類は一致します。このように、右剰余類と左剰余類が等しい場合、右/左を区別することなく単に剰余類といいます。
ですので右剰余類と左剰余類は一致します。このように、右剰余類と左剰余類が等しい場合、右/左を区別することなく単に剰余類といいます。
次の例は加法群
 の部分群
の部分群
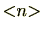 による剰余類が、合同類
による剰余類が、合同類
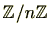 であること示すもので、極めて重要なものです。
であること示すもので、極めて重要なものです。
例 3.1.29
自然数

を固定します。加法群

の部分群
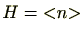
に関する剰余類を検討しましょう。
整数
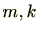
に対し、
したがって、同値関係
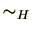
は、
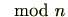
による同値関係と同じです。
よって、剰余類
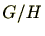
は、
合同類
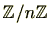
です。
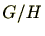 は同値類ですので完全代表系(同値関係
は同値類ですので完全代表系(同値関係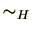 の完全代表系を指します。)
の完全代表系を指します。) がとれます。すると、完全代表系の定義より
がとれます。すると、完全代表系の定義より は
は 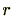 が
が の元を動くとき
の元を動くとき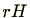 の直和で表せます。つまり、
の直和で表せます。つまり、
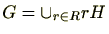 です。
です。
(左剰余類に関しても同様に完全代表系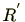 がとれ、同様のことが成り立ちますが、右剰余類の完全代表系とは一般的には異なることに注意しましょう。)
がとれ、同様のことが成り立ちますが、右剰余類の完全代表系とは一般的には異なることに注意しましょう。)
次の定理は重要です。 の位数(元の個数)を
の位数(元の個数)を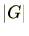 と記載し同様に
と記載し同様に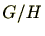 の位数(元の個数)も
の位数(元の個数)も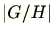 と記載します。
と記載します。
定理 3.1.30

を有限群、
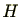
を部分群とするとき
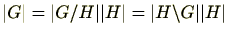
が成り立つ。
特に、
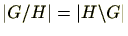
であり、
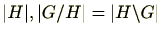
は
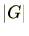
の約数である。
証明
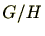
の完全代表系を

とすると、
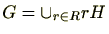
。ここで、
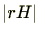
は
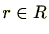
によることなく定まり
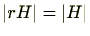
である。また、完全代表系の定義より、
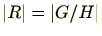
である。
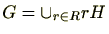
が直和であることより、
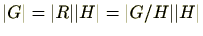
。
左剰余類の場合も同様に示せる。
系 3.1.31

を有限群とすると、

の元
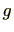
の位数は群

の位数の約数である。
特に、
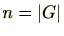
とする
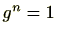
である。
フェルマーの小定理は、この系を合同群の乗法群
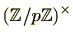 に適用した特別な場合と理解できます。
に適用した特別な場合と理解できます。
Takashi
平成24年5月27日
![]() を群
を群![]() をその部分群とするとき、
をその部分群とするとき、![]() の2元
の2元![]() に対し関係
に対し関係
![]() を、
を、![]() のとき
のとき
![]() であると定義します。
であると定義します。
![]() にはもう1つの関係
にはもう1つの関係
![]() を
を![]() のときに
のときに
![]() と定義することにより上記と同様に同値関係を定義できます。
と定義することにより上記と同様に同値関係を定義できます。
![]() との違いは
との違いは![]() が
が![]() の左側にあるか右側にあるかです。
の左側にあるか右側にあるかです。
![]() と同値関係
と同値関係
![]() は、一般的には異なります。これが同じ関係になるような部分群
は、一般的には異なります。これが同じ関係になるような部分群![]() は大変重要です。
は大変重要です。
![]() に同値関係が定義されましたので、これに関する同値類が定義できます。
に同値関係が定義されましたので、これに関する同値類が定義できます。
![]() がアーベル群のとき、
がアーベル群のとき、![]() ですので右剰余類と左剰余類は一致します。このように、右剰余類と左剰余類が等しい場合、右/左を区別することなく単に剰余類といいます。
ですので右剰余類と左剰余類は一致します。このように、右剰余類と左剰余類が等しい場合、右/左を区別することなく単に剰余類といいます。
![]() の部分群
の部分群
![]() による剰余類が、合同類
による剰余類が、合同類
![]() であること示すもので、極めて重要なものです。
であること示すもので、極めて重要なものです。
![]() は同値類ですので完全代表系(同値関係
は同値類ですので完全代表系(同値関係![]() の完全代表系を指します。)
の完全代表系を指します。)![]() がとれます。すると、完全代表系の定義より
がとれます。すると、完全代表系の定義より![]() は
は ![]() が
が![]() の元を動くとき
の元を動くとき![]() の直和で表せます。つまり、
の直和で表せます。つまり、
![]() です。
です。
![]() がとれ、同様のことが成り立ちますが、右剰余類の完全代表系とは一般的には異なることに注意しましょう。)
がとれ、同様のことが成り立ちますが、右剰余類の完全代表系とは一般的には異なることに注意しましょう。)
![]() の位数(元の個数)を
の位数(元の個数)を![]() と記載し同様に
と記載し同様に![]() の位数(元の個数)も
の位数(元の個数)も![]() と記載します。
と記載します。